DEDICATORIA
- Descartes
- Pascal
- Newton
- Leibniz
- Euler
- Lagrange
- Comte …(¡Alah se compadezca de esos infieles!)
Y también a todos los que estudian, enseñan o admiran la prodigiosa ciencia de las medidas, de las funciones, de los movimientos y de las fuerzas.
Yo “el-hadj” cherif Alí Iezid Izzy-Edin Ibn Salin Hank, MALBA TAHAN (creyente de Alah y de su santo profeta Mahoma), dedico estas páginas, sin valor, de leyenda y fantasía.
En Bagdad, a 19 lunas de Ramadán en 1321.
Biografía de Malba Tahan
El Brasilero Que Hizo Divertida El Álgebra
Andréa Estevão
Su nombre era Júlio César de Mello Souza más conocido como Malba Tahan. Escribió más de 50 libros bajo este seudónimo –incorporado más tarde a su tarjeta de identidad. Empleó historias orientales para enseñar matemáticas. Su libro más famoso, publicado por primera vez en 1938, estuvo recientemente en la lista de los libros más vendidos.
Desde la primera mitad del siglo XX, varias generaciones de brasileros se introdujeron en la cultura Árabe gracias a la influencia del más Árabe de los Cariocas (nativos de la ciudad de Río de Janeiro), el profesor de matemáticas Júlio César de Mello e Souza, más conocido como Malba Tahan.
Su libro más famoso, “O Homem que Calculava” (El Hombre Que Calculaba), trajo aventuras en escenarios Árabes típicos junto con atractivas soluciones de problemas de álgebra y aritmética, ha llegado ya a su edición número 63 de la casa de publicaciones Record de Brasil.
El libro ha alcanzado la hazaña de aparecer todavía en el quinto lugar en las listas de libros para chicos más vendidos publicada en el periódico O Globo, en mayo del año 2004.En total, Júlio César ó Malba Tahan escribió 103 libros, incluyendo textos de ciencia ficción, obras escolares y libros científicos, y ha vendido más de 2.6 millones de copias.
El matemático Júlio César de Mello e Souza se enamoró de la cultura árabe siendo niño, al leer “Las Mil Y Una Noches”. Sin embargo, fue en 1919, a los 23 años de edad, que él se introdujo en el estudio del lenguaje y la cultura Árabes.
Entre 1919 y 1925, se dedicó por cuenta propia a leer el Talmud y el Corán, y a aprender historia y geografía de los países Árabes.
Tal empresa se hizo evidente en la forma en que él desarrolló sus personajes, la sensibilidad con la que tejió sus diálogos llenos de poesía y sabiduría; en la verosimilitud de los escenarios descritos.
Niños y adultos parecen involucrarse completamente en la forma en que el autor les describe las salas suntuosas, o la seducción de una tienda llena de turbantes, joyas o exquisitos tejidos.
Un gran contador de historias, nacido en el Cairo o en Constantinopla en otra época, Júlio César ha sido considerado un auténtico cheik el-medah.
En la presentación de la traducción de “Las Mil y una Noches”, publicada por la casa Ediouro, manifiesta:
" La leyenda es la más delicada expresión de literatura popular. El hombre, en la atractiva ruta de cuentos e historias, intenta escapara a la vulgaridad diaria, embelleciendo la vida con una soñada espiritualidad. "
En una declaración grabada en el Museo de Imagen y Sonido de Río de Janeiro, el profesor Mello e Souza afirma que el opta por escribir fábulas y leyendas como un Árabe cuando ninguna persona ha superado a los Árabes en el arte de contar historias y en la pasión por escucharlas.
Su Debut en el Periódico
Malba Tahan fue presentado al público en Río de Janeiro en 1925, e el periódico A Noite, donde escribió una biografía ficticia traducida supuestamente por un traductor ficticio, Breno Alencar Bianco.
Tanto el escritor como el traductor eran fruto de la prodigiosa creatividad de Júlio César, quien le dio vida y producción literaria en una columna titulada "Los Relatos de Malba Tahan".
El personaje ficticio Ali Lezid Izz Eduim Salim Hark Malba Tahan nació en 1885, en la ciudad de Muzalit, cerca de la Meca, llegando a ser, en su juventud, alcalde de El Medina.
Rico, habiendo heredado la fortuna de su padre, Tahan viajó a varios países incluyendo a Rusia, India, y Japón. En la “biografía”, también se dice que Tahan murió en 1921, en la lucha por la liberación de una tribu en Arabia Central.
Casi todos los 50 libros escritos bajo su seudónimo de Malba Tahan incluyen sheiks, Beduinos, y califas, y ellos se sitúan en el desierto, en hostales, y palacios en Damasco, Bagdad, o en pueblos Persas.
Sus libros narran apasionantes aventuras, llenas de magia –muchas de ellas inspiradas en leyendas y cuentos Árabes- y muchas referencias términos y expresiones típicas, tales como: Allahu Abkar! (¡Allah es el Más Grande!) y en las enseñanzas tradicionales de la cultura Árabe.
Casi resulta incorrecto afirmar que Malba Tahan es el seudónimo usado por Júlio César de Mello e Souza.
En primer lugar, debido a que Júlio César se llamaba a sí mismo Malba Tahan, como lo hizo con sus en el Colegio Pedro II y en el Instituto Para La Educación, e incluso escribía su nombre en caracteres Árabes, mostrando que él había leído las notas de sus estudiantes.
En segundo lugar, debido a que la popularidad del nombre fue tan grande que el presidente de Brasil de ese entonces, Getúlio Vargas, autorizó a Júlio César a poner el nombre en su tarjeta de identidad.
En tercer lugar, debido a que sus publicaciones literarias y sus ideas referentes a la educación y a la ciencia en general, y específicamente a las matemáticas, se refieren internacionalmente a Malba Tahan.
Todo lo que tienes que hacer es buscar en Internet para que veas la importancia dada a Malba Tahan y a su éxito en ventas " El Hombre Que Calculaba", mencionado en varios sitios en varios lenguajes, incluyendo el griego, el alemán y el holandés.
Admirado Por Autores Famosos
El Hombre Que Calculaba, fue publicado por primera vez en 1938, ha sido traducido a más de 12 idiomas, incluyendo el Inglés, tanto el Americano como el Británico, el Español, el Italiano, El Francés, y el Catalán.
Ha recibido premios por la Academia Brasilera de Letras y se ha Ganado la admiración de autores imaginativos y populares incluyendo al Brasilero Monteiro Lobato (muy famoso por los libros infantiles) y al Argentino Jorge Luís Borges –el más reciente enamorado de los cuentos Árabes.
El libro cuenta las aventuras de Beremiz Samir, un hombre con una gran habilidad para los cálculos. Beremiz resolvía problemas y situaciones complicadas de todos los estilos con gran talento, simplicidad, y precisión, de cualquier índole con el uso de las matemáticas.
Júlio César nació el 6 de Mayo de 1895, en la ciudad de Río de Janeiro, y murió en el estado Nordeste de Pernambuco el 18 de Junio de 1974, donde él dio una de sus muchas charlas bastante solicitadas.
El dejó un importante registro de su vida y su trabajo: el libro de sus memorias titulado Acordaram-me de Madrugada (“ Me Levantaron De Madrugada”), y su exposición grabada en el Museo de la Imagen y el Sonido (MIS), en Río de Janeiro.
Antes de morir, pidió ser enterrado sin mucha ceremonia, flores, o coronas, como una persona común del Medio Oriente. Para justificar así su deseo de no llevar luto en su honor, citó los versos del famoso compositor Brasilero Noel Rosa:
"Los vestidos negros son vanidad
Para quienes visten de fantasía
mi luto es la pena
y la pena no tiene color.
Septiembre de 2004
Capítulo 1
En el cual encuentro, durante una excursión, un viajero singular. Qué hacía el viajero y cuáles eran las palabras que pronunciaba.
- Disponíame a dirigir al desconocido el “zalam” [1] trivial de los caminantes, cuando con gran sorpresa le vi levantarse y pronunciar lentamente:
- Un millón cuatrocientos veintitrés mil, setecientos cuarenta y cinco.
Sentóse enseguida y quedó en silencio, la cabeza apoyada en las manos, como si estuviera absorto en profunda meditación.
Me paré a corta distancia y me puse a observarle como lo habría hecho frente a un monumento histórico de tiempos legendarios.
Momentos después se levantó, nuevamente, el hombre, y, con voz clara y pausada, enunció otro número igualmente fabuloso:
- Dos millones, trescientos veintiún mil, ochocientos sesenta y seis.
Y así, varias veces, el extravagante viajero, puesto de pie, decía un número de varios millones, sentándose en seguida en la tosca piedra del camino.
Sin saber refrenar la curiosidad que me aguijoneaba, me aproximé al desconocido, y después de saludarlo en nombre de Alah (con Él en la oración y en la gloria)[2], le pregunté el significado de aquellos números que sólo podrían figurar en proporciones gigantescas.
¡Forastero!, respondió el “Hombre que calculaba”, no censuro la curiosidad que te llevó a perturbar la marcha de mis cálculos y la serenidad de mis pensamientos. Y, ya que supiste ser delicado al hablar y al pedir, voy a satisfacer tu deseo. Para eso necesito, sin embargo, contarte la historia de mi vida.
Y narróme lo siguiente:
Capítulo 2
En el cual Beremís Samir, el “Hombre que calculaba”, cuenta la historia de su vida. Cómo fui informado de los prodigiosos cálculos que realizaba y por qué nos hicimos compañeros de viaje.
Todos los días, al salir el Sol, llevaba el gran rebaño al campo, debiendo ponerlo al abrigo, al atardecer. Por temor de extraviar alguna oveja y ser por tal negligencia castigado, contábalas varias veces durante el día. Fui, así, adquiriendo, poco a poco, tal habilidad para contar que, a veces, instantáneamente, calculaba sin error el rebaño entero. No contento con eso, pasé a ejercitarme contando además los pájaros cuando, en bandadas, volaban por el cielo. Volvíme habilísimo en ese arte. Al cabo de algunos meses –gracias a nuevos y constantes ejercicios-, contando hormigas y otros pequeños insectos, llegué a practicar la increíble proeza de contar todas las abejas de un enjambre. Esa hazaña de calculista nada valdría frente a las otras que más tarde practiqué. Mi generoso amo, que poseía, en dos o tres oasis distantes, grandes plantaciones de dátiles, informado de mis habilidades matemáticas, me encargó de dirigir su venta, contándolos yo uno por uno en los cachos. Trabajé asía al pie de los datileros cerca de diez años. Contento con las ganancias que obtuvo, mi bondadoso patrón acaba de concederme algunos meses de descanso, y por eso voy ahora a Bagdad pues deseo visitar a algunos parientes y admirar las bellas mezquitas y los suntuosos palacios de esa bella ciudad. Y para no perder el tiempo, me ejército durante el viaje, contando los árboles que dan sombra a la región, las flores que la perfuman y los pájaros que vuelan en el cielo, entre las nubes.
Y señalando una vieja y grande higuera que se erguía a poca distancia, prosiguió:
- Aquel árbol, por ejemplo, tiene doscientas ochenta y cuatro ramas. Sabiendo que cada rama tiene, término medio, trescientas cuarenta y siete hojas, se deduce fácilmente que aquel árbol tendrá un total de noventa y ocho mil quinientas cuarenta y ocho hojas. ¿Qué le parece, amigo?
- ¡Qué maravilla! –exclamé atónito-. ¡Es increíble que un hombre pueda contar todos los gajos de un árbol, y las flores de un jardín! Tal habilidad puede proporcionar a cualquier persona un medio seguro de ganar envidiables riquezas.
- ¿Cómo es eso? –preguntó Beremís-, ¡Jamás pasó por mi imaginación que pudiera ganarse dinero contando los millones de hojas de los árboles o los enjambres de abejas! ¿Quién podría interesarse por el total de ramas de un árbol o por el número de pájaros que cruzan el cielo durante el día?
- Vuestra admirable habilidad – expliqué- podría ser empleada en veinte mil casos diferentes. En una gran capital como Constantinopla, o aún en Bagdad, seríais útiles auxiliar para el Gobierno. Podríais calcular poblaciones, ejércitos y rebaños. Fácil os sería evaluar las riquezas del país, el valor de las colectas, los impuestos, las mercaderías y todos los recursos del Estado. Yo os aseguro –por las relaciones que mantengo, pues soy bagdalí [4], que no os sería difícil obtener una posición destacada junto al glorioso califa Al-Motacen (nuestro amo y señor). Podríais, tal vez, ejercer el cargo de visir – tesorero o desempeñar las funciones de Finanzas musulmanas [5].
- Si es así, joven – respondió el calculista- no dudo más, y os acompaño hacia Bagdad.
Y sin más preámbulo, se acomodó como pudo encima de mi camello (único que teníamos), rumbo a la ciudad gloriosa.
De ahí en adelante, ligados por ese encuentro casual en medio del agreste camino, nos hicimos compañeros y amigos inseparables.
Beremís era de genio alegre y comunicativo. Joven aún –pues no tendría veintiséis años-, estaba dotado de gran inteligencia y notable aptitud para la ciencia de los números[6].
Formulaba, a veces, sobre los acontecimientos más banales de la vida, comparaciones inesperadas que denotaban gran agudeza de espíritu y verdadero talento matemático. Beremís también sabía contar historias y narrar episodios que ilustraban sus conversaciones, de por sí atrayentes y curiosas.
A veces pasábase varias horas, en hosco silencio, meditando sobre cálculos prodigiosos. En esas oportunidades me esforzaba por no perturbarlo, quedándome quieto, a fin de que pudiera hacer, con los recursos de su memoria privilegiada, nuevos descubrimientos en los misteriosos arcanos de la Matemática, ciencia que los árabes tanto cultivaron y engrandecieron.
Capítulo 3
Singular aventura acerca de 35 camellos que debían ser repartidos entre tres árabes. Beremís Samir efectúa una división que parecía imposible, conformando plenamente a los tres querellantes. La ganancia inesperada que obtuvimos con la transacción.
Encontramos, cerca de una antigua posada medio abandonada, tres hombres que discutían acaloradamente al lado de un lote de camellos.
Furiosos se gritaban improperios y deseaban plagas:
- ¡No puede ser!
- ¡Esto es un robo!
- ¡No acepto!
El inteligente Beremís trató de informarse de que se trataba.
- Somos hermanos –dijo el más viejo- y recibimos, como herencia, esos 35 camellos. Según la expresa voluntad de nuestro padre, debo yo recibir la mitad, mi hermano Hamed Namir una tercera parte, y Harim, el más joven, una novena parte. No sabemos sin embargo, como dividir de esa manera 35 camellos, y a cada división que uno propone protestan los otros dos, pues la mitad de 35 es 17 y medio. ¿Cómo hallar la tercera parte y la novena parte de 35, si tampoco son exactas las divisiones?
- Es muy simple –respondió el “Hombre que calculaba”-. Me encargaré de hacer con justicia esa división si me permitís que junte a los 35 camellos de la herencia, este hermoso animal que hasta aquí nos trajo en buena hora.
Traté en ese momento de intervenir en la conversación:
- ¡No puedo consentir semejante locura! ¿Cómo podríamos dar término a nuestro viaje si nos quedáramos sin nuestro camello?
- No te preocupes del resultado “bagdalí” –replicó en voz baja Beremís-. Sé muy bien lo que estoy haciendo. Dame tu camello y verás, al fin, a que conclusión quiero llegar.
Fue tal la fe y la seguridad con que me habló, que no dudé más y le entregué mi hermoso “jamal” [7], que inmediatamente juntó con los 35 camellos que allí estaban para ser repartidos entre los tres herederos.
- Voy, amigos míos –dijo dirigiéndose a los tres hermanos- a hacer una división exacta de los camellos, que ahora son 36.
Y volviéndose al más viejo de los hermanos, así le habló:
- Debías recibir, amigo mío, la mitad de 35, o sea 17 y medio. Recibirás en cambio la mitad de 36, o sea, 18. Nada tienes que reclamar, pues es bien claro que sales ganando con esta división.
Dirigiéndose al segundo heredero continuó:
- Tú, Hamed Namir, debías recibir un tercio de 35, o sea, 11 camellos y pico. Vas a recibir un tercio de 36, o sea 12. No podrás protestar, porque también es evidente que ganas en el cambio.
Y dijo, por fin, al más joven:
- A ti, joven Harim Namir, que según voluntad de tu padre debías recibir una novena parte de 35, o sea, 3 camellos y parte de otro, te daré una novena parte de 36, es decir, 4, y tu ganancia será también evidente, por lo cual sólo te resta agradecerme el resultado.
Luego continuó diciendo:
- Por esta ventajosa división que ha favorecido a todos vosotros, tocarán 18 camellos al primero, 12 al segundo y 4 al tercero, lo que da un resultado (18 + 12 + 4) de 34 camellos. De los 36 camellos sobran, por lo tanto, dos. Uno pertenece, como saben, a mi amigo el “bagdalí” y el otro me toca a mí, por derecho, y por haber resuelto a satisfacción de todos, el difícil problema de la herencia [8].
- ¡Sois inteligente, extranjero! –exclamó el más viejo de los tres hermanos-. Aceptamos vuestro reparto en la seguridad de que fue hecho con justicia y equidad.
El astuto beremís –el “Hombre que calculaba”- tomó luego posesión de uno de los más hermosos “jamales” del grupo y me dijo, entregándome por la rienda el animal que me pertenecía:
- Podrás ahora, amigo, continuar tu viaje en tu manso y seguro camello. Tengo ahora yo, uno solamente para mí.
Y continuamos nuestra jornada hacia Bagdad.
Capítulo 4
En el cual encontramos un rico sheik, casi muerto de hambre en el desierto. La propuesta que nos hizo sobre los ocho panes que teníamos y como se resolvió, de manera imprevista, el pago con ocho monedas. Las tres divisiones de Beremís: la división simple, la división exacta y la división perfecta. Elogio que un ilustre visir dirigió al “Hombre que calculaba”.
Socorrímosle y de su labios oímos el relato de su aventura.
Llamábase Salem Nasair, y era uno de los más ricos negociantes de Bagdad. Al regresar, pocos días antes, de Basora, con una gran caravana, fue atacado por una turba de persas, nómades del desierto. La caravana fue saqueada, pereciendo casi todos sus componentes a manos de los beduinos. Sólo se había salvado él, que era el jefe, ocultándose en la arena, entre los cadáveres de sus esclavos.
Al terminar el relato de sus desgracias, nos preguntó con voz angustiosa:
- ¿Tenéis, por casualidad, musulmanes, alguna cosa para comer? ¡Estoy casi muriéndome de hambre!
- Tengo solamente tres panes –respondí.
- Yo traigo cinco –afirmó a mi lado el “Hombre que calculaba”.
- Pues bien –sugirió el sheik [9]-; juntemos esos panes y hagamos una sociedad única. Cuando lleguemos a Bagdad os prometo pagar con ocho monedas de oro el pan que coma.
Así hicimos, y al día siguiente, al caer la tarde, entramos en la célebre ciudad de Bagdad, la perla de Oriente.
Al atravesar una hermosa plaza, nos enfrentamos con un gran cortejo. Al frente marchaba, en brioso alazán, el poderoso Ibraim Maluf, uno de los visires[10] del califa en Bagdad.
Al ver el visir a sheik Salem Nasair en nuestra compañía, gritó, haciendo parar su poderosa escolta, y le preguntó:
- ¿Qué te ha pasado, amigo mío? ¿Por qué te veo llegar a Bagdad sucio y harapiento, en compañía de dos hombres que no conozco?
El desventurado sheik narró, minuciosamente, al poderoso ministro todo lo que le ocurriera en el camino, haciendo los mayores elogios respecto de nosotros.
- Paga sin pérdida de tiempo a esos dos forasteros, ordenó el visir.
Y sacando de su bolsa 8 monedas de oro las entregó a Salem Nasair, insistiendo:
- Quiero llevarte ahora mismo al palacio, pues el Comendador de los Creyentes desea, con seguridad, ser informado de esta nueva afrenta que lo beduinos practicaran, al matar a nuestros amigos saqueando caravanas dentro de nuestras fronteras.
- Voy a dejaros, amigos míos -; dijo Nasair- mas, antes deseo agradeceros el gran servicio que me habéis prestado. Y para cumplir la palabra, os pagaré el pan que tan generosamente me dierais.
Y dirigiéndose al “Hombre que calculaba” le dijo:
- Por tus cinco panes te daré cinco monedas.
Y volviéndose hacia mí, concluyó:
- Y a ti, “bagdalí”, te daré por los tres panes tres monedas.
Con gran sorpresa nuestra, el “Calculista” objetó, respetuosamente:
- ¡Perdón, oh sheik! La división hecha de ese modo será muy sencilla, mas no es matemáticamente exacta. Si yo di 5 panes, debo recibir 7 monedas; y mi compañero, “el Bagdad” que dio tres panes, solamente debe recibir una moneda.
- ¡Por el nombre de Mahoma! [11] –dijo el visir Ibraim, interesado vivamente por el caso-. ¿Cómo justificas, extranjero, tan disparatada forma de pagar 8 panes con 8 monedas? Si contribuiste con 5 panes, ¿por qué exiges 7 monedas? Y si tu amigo contribuyó con 3 panes, ¿por qué afirmas que debe recibir únicamente una moneda?
El “Hombre que calculaba” se aproximó al poderoso ministro y así le habló:
- Voy a probaros que la división de las monedas hecha en la forma propuesta por mí, es más justa y más exacta. Cuando, durante el viaje, teníamos hambre, sacaba un pan de la caja y lo partía en tres trozos, uno para cada uno de nosotros. Todos los panes que eran 8, fueron divididos, pues, en la misma forma. Es evidente, por lo tanto, que si yo tenía 5 panes, di 15 pedazos; si mi compañero tenía 3 panes, dio 9 pedazos. Hubo, así, un total de 24 pedazos, de los cuales cada uno de nosotros comió 8. Ahora bien; si de mis 15 pedazos comí 8, di, en realidad, 7; y mi compañero, que tenía 9 pedazos, al comerse 8, solo dio 1. Los 7 que di yo y el que suministró “el bagdalí” formaron los 8 que comiera el sheik Salem Nasair. Por consiguiente, es justo que yo reciba 7 monedas y mi compañero 1.
El gran visir, después de hacer los mayores elogios al “Hombre que calculaba”, ordenó que le fueran entregadas las 7 monedas, pues a mí sólo me tocaba, por derecho, 1. La demostración lógica y perfecta presentada por el matemático no admitía duda.
- Esa división – replicó entonces el “Calculista”- es matemáticamente exacta, pero a los ojos de Dios no es perfecta.
Y tomando las ocho monedas en la mano las dividió en dos partes iguales. Dióme una de ellas y se guardó la otra.
- Ese hombre es extraordinario –exclamó el visir-. No aceptó la división propuesta de las ocho monedas en dos partes de 5 y 3, en la que salía favorecido; demostró tener derecho a 7 y su compañero a 1, acabando por dividir las 8 monedas en dos partes iguales, que repartió con su amigo.
Y añadió con entusiasmo:
- ¡Mac Alah![12] Ese joven, además de parecerme un sabio habilísimo en los cálculos de Aritmética, es bueno como amigo y generoso como compañero. Tómolo ahora mismo como secretario mío.
- Poderoso visir –le dijo el “Hombre que calculaba”-, veo que acabáis de hacer, con 29 palabras y un total de 145 letras, el mayor elogio que oí en mi vida, y yo, para agradecéroslo, me veo en la obligación de emplear 58 palabras en las cuales figuran nada menos que 290 letras, el doble de las vuestras[13], precisamente. ¡Que Alah os bendiga y proteja!
Con estas palabras el “Hombre que calculaba” nos dejó a todos maravillados de su argucia e invencible talento de calculista.
Capítulo 5
En el cual nos dirigimos a una posada. Palabras calculadas por minuto. Beremís resuelve un problema y determina la deuda de un joyero. Los médicos del rey Artajerjes y la Aritmética.
Allí vendimos nuestros camellos a un chamir[14] de mi confianza, que vivía cerca.
En el camino dije a Beremís:
- Ya veis, amigo, tuve razón cuando afirmé que un calculista hábil hallaría con facilidad un buen empleo en Bagdad. No bien llegasteis, fuisteis invitado a ejercer el cargo de secretario de un visir. Ahora no necesitaréis más volver a la árida y triste aldea de Khoy.
- Aunque aquí prospere me contestó el “Calculista”-, aunque me enriquezca, volveré, con el tiempo a Persia, para ver mi tierra natal. Es ingrato aquel que olvida su patria y los amigos de la infancia., cuando tiene la felicidad de encontrar en su vida un oasis de prosperidad y fortuna. Y añadió:
- Viajamos juntos hasta este momento, exactamente ocho días. Durante ese tiempo, para aclarar dudas e indagar sobre cosas que me interesaban, pronuncié exactamente 414.720 palabras. Ahora bien; como en 8 días hay 11.520 minutos, saco en conclusión que durante nuestro viaje pronuncié, término medio, 36 palabras por minuto, o sea 2.160 por hora. Estos números demuestran que hablé poco, fui discreto y no ocupé tu tiempo haciéndote escuchar discursos engorrosos y estériles. Un hombre taciturno, excesivamente callado, se vuelve desagradable, mas los que hablan sin parar irritan y fastidian a sus oyentes. Debemos, pues, evitar las palabras inútiles, sin caer en el laconismo, que es incompatible con la delicadeza. Había una vez en Teherán, Persia, un viejo mercader que tenía tres hijos. Un día el mercader los llamó y les dijo: “Aquel de vosotros que pase el día sin decir palabras inútiles recibirá un premio de 23 dracmas [15]”. Al caer la noche, los tres hijos se presentaron al anciano. El primero dijo: “Evité hoy, padre mío, todas las palabras inútiles. Espero, por tanto, merecer, según vuestra promesa, el premio estipulado, premio de 23 dracmas, como sin duda recordareis.” El segundo se aproximó al anciano, le besó las manos y se limitó a decir: “Buenas noches, padre mío.” El más joven, en fin, se aproximó al anciano y sin decir palabra extendió la mano para recibir el premio. El mercader, al observar la actitud de los tres muchachos, les habló así: “Fatigóme el primero, al llegar a mi presencia, con varias palabras inútiles. El tercero se mostró demasiado lacónico. El premio corresponde, pues, al segundo, que en su conversación fue discreto y sin afectación.”
Al terminar, Beremís me preguntó:
- ¿No te parece que el viejo mercader falló con justicia al juzgar a sus tres hijos?
No le respondí. Me pareció mejor no discutir el caso de los veintitrés dracmas con aquel hombre prodigioso que calculaba medidas y resolvía problemas, reduciendo todo a números.
Momentos después llegábamos al “Patito Dorado”.
El dueño de la posada se llamaba Salim y había sido empleado de mi padre. Al verme, gritó sonriente:
- ¡Alah sea contigo, mi señor! [16] Aguardo tus órdenes ahora y siempre.
Díjele entonces que necesitaba una habitación para mí y para mi amigo Beremís Samir, el calculista, secretario del visir Maluf.
- ¿Ese hombre es un calculista? -exclamó el viejo Salim-. Sí así es, llegó en un momento oportuno para sacarme de un apuro. Acabo de tener una seria divergencia con un joyero. Discutimos largo rato, y de nuestra discusión ha resultado, al final, un problema que no sabemos resolver.
Al saber que un calculista había llegado a la posada, varias personas se aproximaron, curiosas. El vendedor de joyas fue llamado, y declaró estar interesadísimo en la resolución de ese problema.
- ¿Cuál es el origen de la duda? –preguntó Beremís.
El viejo Salim contestó:
- Ese hombre, y señaló al joyero, vino desde Siria a vender joyas en Bagdad, prometiéndome pagar por el hospedaje veinte dracmas si vendía las joyas por 100 dracmas, pagando 35 si las vendía por 200.
Proporción que planteó el mercader de joyas: 200 : 35 = 140 : x El valor de x es 24,5 |
Al cabo de varios días de ir y venir de aquí para allá, vendió todo en 140 dracmas. ¿Cuánto debe pagar, en consecuencia, ateniéndose a lo convenido, por concepto de hospedaje?
- Debo pagar apenas 24 dracmas y medio –replicó el mercader sirio-. Si vendiendo a 200 pagaría 35, vendiendo a 140 debo pagar 24 y medio.
- Está equivocado –replicó irritado el viejo Salim-. Por mis cálculos son 28. vea usted: si por 100 debía pagar 20, por 140 debo recibir 28.
Proporción que planteó el dueño de la hospedería: 100 : 20 = 140 : x El valor de x es 28 |
- Calma, mis amigos –interrumpió el calculista- es preciso encarar las dudas con serenidad y bondad. La precipitación conduce al error y a la discordia. Los resultados que los señores indican están equivocados, según voy a demostrarlo:
Y aclaró el caso del siguiente modo:
- De acuerdo con la combinación hecha, el sirio pagaría 20 dracmas si vendiese las joyas por 100, y se vería obligado a pagar 35 si las vendiese en 200.
Tenemos así:
Precio de venta | Precio hospedaje | ||
200 | 35 | ||
100 | 20 | ||
Diferencia: | 100 | 15 |
Observen que a una diferencia de 100 en el precio de venta, corresponde una diferencia de 15 en el precio del hospedaje. ¿Está claro esto?
- Claro como leche de camello –asintieron ambos.
- Ahora –prosiguió el calculista-, si un acrecentamiento de 100 en la venta produce un aumento de 15 en el hospedaje, un acrecentamiento de 40 (que es los dos quintos de 100) debe producir un aumento de 6 (que es los dos quintos de 15) a favor del posadero. El pago que corresponde a los 140 dracmas es, pues, 20 más 6, o sea, 26.
Proporción que planteó el calculista: 200 : 15 = 40 : x El valor de x es 6 |
Dirigiéndose entonces al joyero sirio, así le habló:
- Mi amigo. Los números, a pesar de su simplicidad aparente, no es raro que engañen, aun al más capaz. Las proporciones, que nos parecen perfectas, nos conducen, a veces, a error. De la incertidumbre de los cálculos es que resulta indiscutible el prestigio de la Matemática. De los términos del problema resulta que el señor deberá pagar a hotelero 26 dracmas y no 24 y medio, como al principio sostenía. Hay todavía una pequeña diferencia que no merece ser considerada y cuya magnitud no puedo expresar numéricamente, por carecer de recursos. [17]
- El señor tiene razón –asintió el joyero-. Reconozco que mi cálculo estaba equivocado.
Y sin dudar, sacó de su bolsa 26 dracmas y los entregó al viejo Salim, ofreciendo como presente al talentoso Beremís un hermoso anillo de oro con dos piedras oscuras, acompañando el obsequio con expresiones afectuosas.
Todos los que se hallaban en la posada admiraron la sagacidad del nuevo calculista, cuya fama, día a día, ganaría a grandes pasos la “almenara” [18] del triunfo.
Momentos después, cuando nos encontrábamos a solas, interrogué a Beremís sobre el sentido exacto de una de sus afirmaciones: “De la incertidumbre de los cálculos es que resulta indiscutible el prestigio de la Matemática”.
El “Hombre que calculaba” me aclaró el concepto:
- Si los cálculos no estuvieran sujetos a dudas y contradicciones, la Matemática sería, al final, de una simplicidad insípida, tibia, apagada, sin interés alguno. No habría raciocinio, ni sofismas, ni artificios; la teoría más interesante desaparecería entre las nebulosidades de las nociones inútiles. Presentándose, sin embargo, aún en las fórmulas más perfectas y rígidas, las dudas, incertidumbres y contradicciones, el matemático toma del carcaj de su inteligencia, sus armas y se apresta a combatir. Donde el ignorante ve incertidumbre y contradicciones, el geómetra demuestra que existe firmeza y armonía. El rey Artajerjes preguntó, cierta vez, a Hipócrates de Cos, médico famoso, como debía proceder para combatir de modo eficiente las epidemias que diezmaban al ejército persa. Hipócrates respondió: “Obligad a todo vuestro cuerpo médico a estudiar Aritmética. Al practicar el estudio de los números y las figuras, los doctores aprenderán a razonar, desenvolviendo sus facultades de inteligencia, y aquel que razona con eficacia es capaz de hallar los medios seguros para combatir cualquier epidemia.”
Capítulo 6
En el cual vamos al palacio del visir Maluf. Encontramos al poeta Iezid, que no reconoce los prodigios del cálculo. “El hombre que calculaba” cuenta, en forma original, una caravana numerosa. La edad de la novia y un camello sin oreja. Beremís descubre la “amistad cuadrática” y habla del rey Salomón.
Al entrar en la hermosa morada del visir, el calculista quedó encantado.
Era una casa principesca, de puro estilo árabe, con un pequeño jardín sombreado por filas paralelas de naranjos y limoneros. Del jardín se pasaba a un patio interior por una estrecha puerta y un corredor que tenía apenas el ancho de un hombre normal. En el fondo del patio erguíanse doce columnas blancas, unidas por otros tantos arcos en forma de herradura, que sostenían, a la altura del primer piso, una galería con baranda de madera. El piso del patio, de la galería y de las habitaciones estaba embaldosado con espléndidos mosaicos de cuadritos esmaltados, de variados colores; los arcos lucían arabescos y pinturas sugestivas; la balaustrada tenía labrados de motivos delicados; todo estaba diseñado con una armonía y una gracia digna de los arquitectos de la Alhambra.
Había en el medio del patio una fuente y, más adelante, otra, revestidas de mosaico con rosas y estrellas y en ella tres surtidores. Del medio de cada arco colgaba una lámpara morisca. Todo era allí, fastuoso y señorial. Una de las alas del edificio, que se extendía a lo largo del jardín, tenía también un frente formado por tres arcos, ante los que susurraba una tercera fuente. En las salas principales, ricos tapices de oro lucían, suspendidos de las paredes.
Ante el gran ministro nos condujo un esclavo negro. Lo encontramos reclinado en grandes almohadones, hablando con dos de sus amigos.
Uno de ellos era el sheik Salem Nasair, nuestro compañero de aventuras en el desierto; el otro era un hombre bajo, de fisonomía bondadosa, de rostro redondo y barba ligeramente grisácea. Vestía con esmerado gusto y lucía en el pecho, una medalla de oro de forma rectangular, que tenía una cara del color del oro y otra obscura como bronce.
Nos recibió el visir Maluf con demostraciones de viva simpatía, y dirigiéndose al hombre de la medalla, le dijo sonriente:
- Aquí está, caro Iezid, nuestro gran matemático. El joven que lo acompaña es un “bagdalí” que lo descubrió por casualidad cuando viajaba por los caminos de Alah.
Dirigimos un respetuoso “zalam” al noble jefe. Más tarde supimos que se trataba de un poeta brillante –Iezid Abul -Hamid-, amigo y confidente del califa Al-Motacen.
La singular medalla la había recibido de sus manos como premio, por haber escrito un poema de treinta mil doscientos versos sin emplear una sola vez, las letras “kaf”, “lam” y “ayu” [20].
- Amigo Maluf –dijo el poeta Iezid-, cuéstame creer las hazañas prodigiosas llevadas a cabo por este calculista persa. Cuando se combinan los números, aparecen, también, los artificios del cálculo y las mistificaciones algebraicas. Presentóse cierta vez un mago, que afirmaba poder leer el destino de los hombres en la arena, al rey El-Harit, hijo de Modad. –“¿Hace usted cálculos?”, le preguntó el rey. Y antes de que el mago saliese de su asombro, continuó: “Si no hace cálculos, sus predicciones nada valen; mas si las obtiene por los cálculos, dudo de ellas.” Aprendí en la India un proverbio que dice: “Es preciso desconfiar siete veces del cálculo y cien del calculista.”
- Para poner fin a esas de desconfianzas –sugirió el visir- vamos a someter a nuestro huésped a una prueba decisiva.
Y diciendo así se levantó de los almohadones y nos condujo a una de las ventanas del palacio.
Daba esa ventana para un gran patio que, en ese momento, estaba lleno de camellos.
Eran todos muy hermosos, pareciendo de buena raza; distinguí entre ellos dos o tres blancos, de Mongolia, y varios “carehs”, de pelo claro.
- Es esa –dijo el visir- una hermosa partida de camellos que he comprado y que pienso enviar como dote al padre de mi novia. Di, sin error, cuántos son.
El visir, para hacer más interesante la prueba, dijo en secreto a su amigo Iezid, el número total de animales.
Quiero ahora –prosiguió, volviéndose a Beremís- que nuestro calculista nos diga cuántos camellos hay en el patio, delante de nosotros.
Esperé aprensivo el resultado. Los camellos eran muchos y se confundían en medio de la agitación en que se hallaban. Si mi amigo, en un descuido, errase el cálculo, terminaría nuestra visita, en consecuencia, con el más grande de los fracasos.
Después de dar un vistazo a todos los camellos, el inteligente Beremís dijo:
- Señor visir: creo que se encuentran ahora en el patio, 257 camellos.
- Es verdad –confirmó el visir-: ha acertado. El total es ese, precisamente: 257.
- ¿Cómo llegó al resultado con tanta rapidez y precisión? –preguntó con grandísima curiosidad el poeta Iezid.
- Muy simplemente –explicó Beremís-. Contar los camellos uno por uno, sería, a mi modo de ver, tarea sin importancia, una bagatela. Para hacer más interesante el problema, procedí de la siguiente manera: conté primero todas las patas y después todas las orejas, hallando de ese modo un total de 1.541. A ese resultado sumé una unidad y dividí por 6. Hecha esa división, hallé como cociente exacto, 257.
- ¡Por el nombre del profeta! –exclamó el visir-. Todo esto es originalísimo, admirable. ¡Quién iba a imaginar que este calculista, para hacer más interesante el problema, fuese capaz de contar todas las patas y orejas de 257 camellos! ¡Por la gloria de Mahoma!
- Debo decir, señor ministro –retrucó Beremís-, que los cálculos se vuelven a veces complicados y difíciles como consecuencia de un descuido o de la falta de habilidad del propio calculista. Cierta vez en Khói, en Persia, cuando vigilaba el rebaño de mi amo, pasó por el cielo una bandada de mariposas. “Preguntóme, a mi lado, un pastor, si podía contarlas.” “Son ochocientas cincuenta y seis” –respondí. “¡Ochocientas cincuenta y seis!” respondió mi compañero, como si hubiese exagerado el total. –Fue entonces que noté que por descuido había contado, no las mariposas, sino sus alas. Después de dividir por 2, le dije el resultado verdadero.
Al oír el relato de ese caso, lanzó el visir estrepitosa carcajada, que sonó en mis oídos como si fuera una música deliciosa.
- Hay, sin embargo –insistió muy serio el poeta Iezid- una particularidad que escapa a mi raciocinio. Dividir por 6 es aceptable, ya que cada camello tiene 4 patas y 2 orejas, cuya suma (4+2) es igual a 6 [21]. No obstante, no comprendo por qué razón antes de dividir sumó una unidad al total.
- Nada más simple –respondió Beremís-. Al contar las orejas noté que uno de los camellos era defectuoso (sólo tenía una oreja). Para que la cuenta fuese exacta era, pues, necesario aumentar uno al total obtenido.
Y volviéndose hacia el visir, preguntó:
- ¿Sería indiscreción o imprudencia de mi parte preguntaros, señor, cuál es la edad de aquella que tiene la ventura de ser vuestra novia?
- De ningún modo –respondió sonriente el ministro-. Asir tiene 16 años.
Y añadió, subrayando las palabras con un ligero tono de desconfianza:
- Pero no veo relación alguna, señor calculista, entre la edad de mi novia y los camellos que voy a ofrecer como presente a mi futuro suegro.
- Deseo apenas –refutó Beremís- haceros una pequeña sugestión. Si retiraseis del conjunto, el camello defectuoso (sin oreja), el total sería 256. Ahora bien: 256 es el cuadrado de 16, o sea, 16 veces 16. El presente ofrecido al padre de la encantadora Asir tomará, de ese modo, alto significado matemático. El número de camellos que forman la dote será igual al cuadrado de la edad de la novia. Además el número 256 es potencia exacta del número 2 (que para los antiguos era número simbólico), mientras que 257 es primo[22]. Esas relaciones entre los números cuadrados son buen augurio para los enamorados. Cuéntase que el rey Salomón, para asegurar la base de su felicidad, dio a la reina de Saba –la famosa Balkis- una caja con 529 perlas. Es precisamente 529 el cuadrado de 23, que era la edad de la reina. El número 526 presenta, no obstante, gran ventaja sobre el 529. Si sumamos los guarismos de 256 obtenemos 13, que elevado al cuadrado da 169; la suma de las cifras de ese número es 16, cuyo cuadrado nos reproduce precisamente, 256. Por ese motivo los calculistas llaman reversible al número 256. Existe, pues, entre los números 13 y 16 curiosa relación, que podría ser llamada “amistad cuadrática”. Realmente, si los números hablasen podríamos oír la siguiente conversación: El dieciséis diría al trece:
“Quiero ofrecerte mi homenaje, amigo.
Mi cuadrado es 256, cuya suma de guarismos es 13.”
Y el trece respondería:
“Agradezco tu bondad y quiero retribuirla en la misma forma. Mi cuadrado es 169, cuya suma de guarismos es 16.”
El calculista agregó:
- Creo haber justificado plenamente la preferencia que debe ser otorgada al número 256, que excede en propiedades al 257.
- Su idea es bastante curiosa – acordó prontamente el visir- y voy a adoptarla, aunque caiga sobre mí la acusación de plagiario, del rey Salomón.
Y dirigiéndose al poeta Iezid, concluyó:
- Veo que la inteligencia de este calculista no es menos que su habilidad para descubrir analogías e inventar leyendas. Estuve muy acertado en el momento en que decidí ofrecerle ser mi secretario.
- Siento decirle, ilustre mirza [23] –replicó Beremís- que sólo podría aceptar vuestra honrosa invitación si aquí hubiera lugar para mi buen amigo Hank-Tad-Madya –el “bagdalí”-, que se encuentra en estos momentos sin recursos y sin empleo.
Quedé encantado con la delicadeza del calculista, que procuraba, de esa manera, atraer sobre mí la valiosa protección del poderoso visir.
- Es muy justo su pedido –dijo condescendientemente el ministro-, y su compañero Hank-Tad-Madya se quedará también aquí, ejerciendo las funciones de escribiente, como ya lo he ordenado.
Acepté, sin dudar, la propuesta, expresando después al visir y también al bondadoso Beremís mi reconocimiento.
Capítulo 7
En el cual vamos a la calle de los mercaderes. Beremís y el turbante azul. El caso de los cuatro cuatros. El problema del mercader sirio. Beremís explica todo y es generosamente recompensado. Historia de la “prueba real” del rey de Yemen.
Aquella tarde, la ciudad presentaba un aspecto febril, fuera de lo común. Era que por la mañana habían llegado dos grandes caravanas de Damasco.
Los bazares aparecían llenos de gente; los patios de los almacenes estaban atestados de mercaderías; los fieles rezaban en las puertas de las mezquitas. Por todas las calles se veían los turbantes blancos de los forasteros, y no eran solo los turbantes los que nos parecían blancos, sino que todo se nos presentaba de ese color; daba la impresión de que la gente caminara en puntas de pies. Todo estaba impregnado de un fuerte aroma de áloe, de especias, de incienso, de mirra; parecía que se anduviera por una inmensa droguería.
Los vendedores pregonaban sus mercaderías, aumentando su valor con elogios exagerados, para los que es tan fértil la imaginación árabe.
- ¡Este rico tejido, es digno del profeta!
- Amigo. ¡Es un delicioso perfume, que aumentará el cariño de vuestra esposa!
- Reparad, oh sheik, en estas chinelas y en este lindo “cafetán”[25] que los dijins [26] recomiendan a los ángeles.
Se interesó Beremís por un elegante y armonioso turbante azul claro, que un sirio, medio jorobado, ofrecía por 4 dracmas. La tienda de ese mercader era muy original, pues todo allí (turbantes, cajas, pulseras, puñales, etc.) se vendía por 4 dracmas. Había un letrero que, en caracteres árabes decía:
Los cuatro cuatros
Al ver a Beremís interesado en adquirir el turbante azul, objeté:
- Juzgo una locura el comprar ese lujo. Tenemos poco dinero y no hemos pagado aún el hospedaje.
- No es el turbante lo que me interesa –retrucó Beremís-; observo que la tienda de este mercader se llama “Los cuatro cuatros”. Hay en ello una gran coincidencia, digna de mi atención.
- ¿Coincidencia? ¿Por qué?
- En este momento, “bagdalí” –replicó Beremís- la leyenda que figura en ese letrero me recuerda una de las maravillas del cálculo. Podemos formar un número cualquiera, empleando solamente cuatro cuatros, ligados por signos matemáticos.
Y antes de que le interrogase sobre aquel enigma, Beremís explicó, dibujando en la fina arena que cubría el piso:
- Quiero formar el número cero. Nada hay más simple. Basta escribir:
44-44 = 0
Están así los cuatro cuatros formando una expresión igual a cero.Pasamos ahora al número 1. Esta es la forma más cómoda:
- ¿Cómo formareis el número 4? –pregunté.
- Muy fácilmente –dijo Beremís-. El número cuatro puede formarse de varias maneras; una de ellas sería la siguiente:
Noté entonces que el mercader sirio seguía atento, sin perder palabra, la explicación de Beremís, como si mucho le interesasen las expresiones aritméticas formadas por los cuatro cuatros.
Beremís continuó:
- Para formar el número 5, por ejemplo, no hay dificultad. Escribimos:
4 + 4 + 4 – 4 = 8
El nueve no deja de ser interesante:
- Por lo que acabo de oír, el señor es hábil para sacar cuentas y hacer cálculos. Le regalaré este bello turbante, como presente, si se sirve explicarme cierto misterio que encontré en una suma, y que me tortura desde hace dos años.
Y el mercader narró lo siguiente:
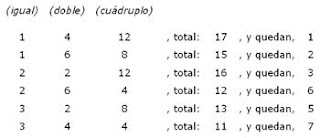
- Presté, cierta vez, la cantidad de 100 dracmas: 50 a un sheik y los otros 50 a un judío de El Cairo.
El sheik pagó su deuda en cuatro cuotas, del modo siguiente:
Pagó | 20, | quedó | debiendo | 30 |
Pagó | 15, | quedó | debiendo | 15 |
Pagó | 10, | quedó | debiendo | 5 |
Pagó | 5, | quedó | debiendo | 0 |
Suma | 50 | Suma | 50 |
- Fíjese, mi amigo continuó el mercader-, en que tanto la suma de las cuotas pagadas como la de los saldos deudores es igual a 50.
El judío pagó también los 50 dracmas en cuatro cuotas, del modo siguiente:
Pagó | 20, | quedó | debiendo | 30 |
Pagó | 18, | quedó | debiendo | 12 |
Pagó | 3, | quedó | debiendo | 9 |
Pagó | 9, | quedó | debiendo | 0 |
Suma | 50 | Suma | 51 |
En este caso la primera suma es 50 (como en el caso anterior), mientras que la segunda da un total de 51.
No sé explicarme esa diferencia de 1 que se observa en la segunda parte del pago. Se bien que no salí perjudicado (pues recibí el total de la deuda), mas ¿cómo justificar el hecho de ser la segunda suma igual a 51 y no a 50?
- Amigo mío –aclaró Beremís-, esto se explica con pocas palabras. En las cuentas de pago, los saldos deudores nada tienen que ver con el total de la deuda. Admitamos que una deuda de 50 fuese pagada en tres cuotas: la primera de 10, la segunda de 5 y la tercera de 35. Efectuemos las sumas:
Pagó | 10, | quedó | debiendo | 40 |
Pagó | 5, | quedó | debiendo | 35 |
Pagó | 35, | quedó | debiendo | 0 |
Suma | 50 | Suma | 75 |
En este ejemplo, la primera suma es 50, mientras que la de los saldos es 75; podía también haber resultado igual a 80, 99, 100, 260, 8000 u otro número cualquiera. Puede por casualidad dar 50 (como en el primer caso), ó 51 (como en el caso del judío).
Quedó conforme el mercader al haber entendido el asunto, cumpliendo su promesa de ofrecer, como presente, al calculista, el turbante azul que valía 4 dracmas.
Beremís, para distraer al buen mercader, le contó enseguida este curioso episodio:
- Omeya, rey de Yemen, tenía un tesorero llamado Quelal, que parecía muy cuidadoso y probo. Queriendo el monarca asegurarse de la honestidad de su auxiliar, hizo lo siguiente: durante tres días colocó, sin decir nada, un dracma en la caja de los gastos. Resultaba claro que el tesorero, al finalizar el día, cuando hiciera el arqueo, hallaría el exceso de un dracma, que anotaría como saldo en el libro correspondiente. El rey observó que en los tres días el tesorero no registraba aquella diferencia. –“Naturalmente que, el muy ambicioso, se guarda el dracma excedente”, supuso el rey. “¡Quien iba a imaginar que el tesorero Quelal fuese capaz de tal proceder!” Resolvió, sin embargo, someterlo a una verdadera prueba, esto es, a una “prueba real”. ¿Y qué hizo el rey? Pues, durante los tres días siguientes retiró secretamente de la caja un dracma, y esperó que el tesorero se diese cuenta y reclamase la diferencia. Pero eso tampoco dio resultado. Mediante esas pruebas, que consideró suficientes, Omeiá llamó su gran visir y le dijo: “Es preciso hacer con urgencia un interrogatorio. Tengo serias razones para desconfiar de nuestro tesorero Quelal.” –“Creo, mi rey, que es necesario investigar”-replicó el visir-. Puedo probar que el indigno Quelal no procede con honestidad.” “¿Cómo?”, preguntó el rey. – Dijo entonces el ministro: “Sepa Vuestra Majestad que resolví, una vez, saber si eran exactas o no las cuentas presentadas diariamente por el tesorero de la Corte. Sin decir nada, durante tres días, retiré de la caja la cantidad de un dracma. Pues bien, el tesorero nunca anotó lo que yo retiraba. A continuación, y también durante tres días, coloqué un dracma en la caja de Quelal, sin que él registrara ese exceso. Ahora bien: cuando un tesorero no anota con exactitud las diferencias de caja, es porque su forma de proceder se aparta de los principios de la más elemental honestidad.” Con sobrada razón se asombró el rey al oír el relato del gran visir. Estaba sí explicado el misterio del caso. Las leyes del Destino son insondables. Por extraordinaria coincidencia, los mismos días en que él ponía un dracma, el visir retiraba la misma cantidad de la caja. El rey no hizo otra cosa, en los días siguientes, que retirar al diligente Quelal el dinero colocado por el astuto ministro. Avergozóse entonces el digno monarca, por el espionaje a que sometiera a un funcionario tan fiel y que tanta lealtad y dedicación había demostrado siempre, así como de haber empleado esos ardides y fraudes, que fueran anulados, empleando iguales medios, por el visir. Cuando el ministro terminó el relato, el poderoso rey se levantó y dijo, mirándolo fijamente: “Sus palabras, visir, solo prueban que nuestro tesorero Quelal es escrupuloso y honestísimo en sus funciones. Resuelvo, pues, que no se haga el interrogatorio, y que Quelal quede en su puesto con el mismo cargo y doble sueldo. El visir, al oír esa inesperada sentencia del rey, tuvo un ataque al corazón y cayó fulminado sobre las gradas del trono. Y no era para menos. ¡Uassalam! [27]
Capítulo 8
En el cual Beremís habla de las formas geométricas. Encontramos al sheik Salen Nasair entre los vendedores de vino. Beremís resuelve el problema de los 21 vasos y otro más que causa asombro a los mercaderes. Un camello robado, descubierto por Geometría. Habla del sabio Al-Hossein, que inventó la “prueba del nueve”.
Está muy bien arreglado –decía, haciendo girar el turbante y examinándolo cuidadosamente por todos lados-. Tiene, para mí manera de ver, un pequeño defecto que pudo ser evitado. Su forma no es rigurosamente geométrica.
Quedé atónito, sin poder disimular la sorpresa que sus palabras me causaran.
Aquel hombre, a más de ser un calculista original, tenía la manía de transformar las cosas más vulgares, de modo de darle forma geométrica hasta a los turbantes de los musulmanes.
- No le admire, amigo mío –prosiguió el inteligente persa-, que yo quiera ver turbantes de forma geométrica [28]. La geometría existe en todas partes. Procure observar las formas regulares y perfectas que presentan algunos cuerpos.
Las flores, las hojas y muchos animales revelan simetrías admirables que deslumbran nuestro espíritu. La Geometría, repito, existe en todas partes. En el disco del Sol, en la hoja del datilero, en el arco iris, en la mariposa, en el diamante, en la estrella de mar y hasta en un pequeño grano de arena. Hay, en fin, infinita variedad de formas geométricas presentadas por la Naturaleza. Un cuervo, al volar lentamente por el cielo, describe figuras admirables; la sangre que circula por las venas de los camellos no escapa a los rigurosos principios geométricos [29]; la piedra que se tira al importuno chacal, dibuja en el aire una curva perfecta [30].
“El beduino ve las formas geométricas, pero no las entiende; el sunita las entiende mas no las admira; el artista, finalmente, mira la perfección de las figuras, comprende lo bello y admira el orden y la armonía”. En el dibujo que ilustra esta página se ve una flor en la que se destaca, en forma impecable, la simetría pentagonal.
La abeja construye sus alvéolos en forma de prismas hexagonales, y adopta esa forma geométrica, creo, para obtener mayor rendimiento y economía de material. La Geometría existe, como dijo el filósofo, en todas partes. Sin embargo, es preciso saber verla, tener inteligencia para comprenderla y alma para admirarla. El rudo beduino, ve las formas geométricas, mas no las comprende; el “sunita”[31] las entiende pero no las admira; el artista, finalmente, mira la perfección de las figuras, comprende lo bello y admira el orden y la armonía. Dios fue un gran geómetra. Geometrizó la Tierra y el Cielo [32]. Existe en Persia una planta, el “saxahul”, muy apreciada como alimento para los camellos y ovejas, cuya semilla…Iba a proseguir el elocuente calculista con sus consideraciones sobre las formas geométricas de las semillas del “saxahul”, cuando vimos en la puerta de una tienda próxima, a nuestro protector, el sheik Salerm Nasair, que nos llamaba a grandes voces.
- Me siento feliz de haberlo encontrado, calculista (exclamó el sheik al aproximársenos); su presencia es muy oportuna. Estoy aquí en compañía de algunos amigos y me hallo azorado con dos problemas que sólo un gran matemático podría resolver.
Aseguró Beremís que emplearía todos sus recursos para hallar la solución de los problemas que interesaban al sheik, pues no quería desperdiciar una sola ocasión de servir a un hombre tan amable y generoso.
El sheik señaló a los tres árabes que lo acompañaban y dijo:
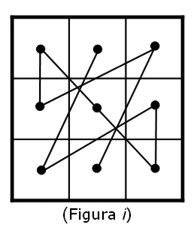
- Estos tres hombres recibirán, como pago de un servicio hecho, una partida de vino compuesta de 21 vasos iguales, estando 7 llenos, 7 medio llenos y 7 vacíos. Quieren ahora dividir los 21 vasos de manera que cada uno reciba el mismo número de vasos y la misma cantidad de vino. ¿Cómo hacer el reparto? Ese es el primer problema.
Esta figura indica, claramente, la solución del problema de los 21 vasos. Los siete primeros rectángulos representan los vasos llenos; los 7 siguientes rectángulos representan los vasos medio llenos y los otros 7 vasos vacíos. Para que los tres mercaderes reciban el mismo número de vasos y cantidades iguales de vino, la división deberá efectuarse cómo indican las líneas punteadas del dibujo.
Pasados algunos minutos de silencio, Beremís respondió:- La división que acabáis de proponer se puede hacer de varias maneras. Indicaré una de ellas. El primer socio recibirá:
3 vasos llenos,
1 medio lleno,
3 vasos vacíos.
2 vasos llenos,
3 medio lleno,
2 vasos vacíos.
2 vasos llenos,
3 medio lleno,
2 vasos vacíos.
La espiral logarítmica se presenta con frecuencia en la naturaleza. Así, por ejemplo, en el girasol aparece dicha curva notable.
Se aproximó uno de los árabes a Beremís y lo saludó respetuosamente hablando así:- Es mucho más difícil el problema que me preocupa. Tengo continuas transacciones con los cristianos que negocian en vinos de Ispahán. Se vende ese vino en vasos pequeños y grandes. Según nuestra invariable combinación, un vaso grande lleno vale 6 vasos pequeños vacíos; dos vasos grandes vacíos valen uno pequeño lleno. Procuro ahora saber cuántos vasos pequeños vacíos puedo cambiar por la cantidad de vino contenida en dos vasos grandes.
Aquel embrollo de valores y relaciones no intimidaron al “Hombre que calculaba”. Habituado a enfrentarse a problemas difíciles y a trabajar con números enormes, Beremís nos se confundía con el enunciado de cuestiones abstrusas y aparentemente sin sentido.
- Amigo mío –respondió, dirigiéndose al vendedor de vinos-. Tengo gran placer en aclarar esta cuestión que me parece tan sencilla como la primera. Por lo que he oído, “2 vasos grandes llenos valen 12 pequeños vacíos”. Por otra parte, si 2 grandes vacíos valen 1 pequeño lleno, y 3 pequeños vacíos valen también 1 pequeño lleno, está claro que 2 grandes vacíos valdrán 3 pequeños vacíos. Es preciso ahora, para mayor claridad, recordar de memoria los dos resultados ya obtenidos:
2 vasos grandes llenos valen 12 pequeños vacíos
2 vasos grandes vacíos valen 3 pequeños vacíos
Es notable la variedad de formas geométricas que se presentan en los organismos vivos. En la figura vemos la “hélice cónica” rigurosamente dibujada en el perfil de un caracol.
Conclusión: La cantidad de vino contenida en dos vasos grandes puede ser permutada por 9 vasos pequeños vacíos.La solución presentada por Beremís asombró a los comerciantes en vinos. Ninguno de ellos suponía que la imaginación de mi amigo fuese capaz de realizar ese prodigio.
Uno de los compañeros del sheik ofreció un poco de vino a Beremís. Este, sin embargo, como buen musulmán, agradeció el ofrecimiento pero no lo aceptó. La bebida es un pecado, y perjudica grandemente la salud y la inteligencia. Y, a fin de evitar que los mercaderes se sintiesen ofendidos con su rechazo, relató lo siguiente:
Figura trazada por Avicena, matemático y médico famoso, con la que pretendía demostrar cierta proposición de Euclides, y concluyó, según reza la leyenda, descubriendo el camello robado.
- Al-Hossein[34], médico y matemático famoso, al llegar a Ispahán, después de una larga excursión, encontró un grupo de hombres que charlaban a la sombra de un gigantesco “betoum”[35]. El sabio, que se hallaba en ese momento alegre y bien dispuesto, resolvió enseñar alguna cosa útil e interesante a los desconocidos. Acercóse a ellos, y, después de saludarlos con simpatía, dijo:- Amigos míos. Existe una ciencia notable y muy útil a los hombres. Con la ayuda de ella se descubre todos los secretos y se revela la verdad. Esa ciencia es la Matemática. Voy a demostraros, en pocas palabras, en que radica su belleza y su poder.
Y después de proferir estas palabras, que no fueron comprendidas por sus rudos oyentes, Al-Hossein tomó un pedazo de carbón y trazó en el tronco de un árbol dos rectas cruzadas. Pretendía el sabio demostrar, con auxilio de esa figura, una propiedad enunciada por Euclides, geómetra griego: “Dos ángulos opuestos por el vértice son iguales”.
La espiral logarítmica puede notarse en gran número de estos seres vivos. Las flores, las hojas y muchos animales revelan simetrías admisibles que maravillan el espíritu. Como dijo Platón, “la Geometría existe en todas partes”.
Después de trazar las rectas en posición conveniente, Al-Hossein marcó con cuidado los dos ángulos cuya igualdad pretendía demostrar con su admirable raciocinio.No había terminado la figura geométrica, cuando uno de los dos camelleros se levantó de súbito y se arrojó trémulo a los pies del sabio, murmurando con voz ronca, que expresaba gran temor:
- ¡Fui yo, señor! ¡Fui yo! ¡Diré la verdad!
Realmente sorprendido con la inesperada actitud del beduino, Al-Hossein se dio cuenta de que había, en la confusión del camellero, un misterio que convenía conocer. Dominando, pues, la sorpresa que experimentara, dijo así:
- Nada debes temer, amigo mío. La verdad es siempre descubierta. Vamos, confiesa todo y serás perdonado.
En el perfil de ciertas palmeras se observa una curva que los matemáticos estudian y analizan minuciosamente: es la curva logarítmica. Esta forma es adoptada por principio de economía, pues el vegetal, de ese modo, con menos cantidad de material, resiste mejor el impulso del viento. El ingeniero, después de laboriosas aplicaciones de cálculo infinitesimal, demuestra que la curva logarítmica es el perfil más conveniente para los faros.
Al oír estas palabras, el hombre confesó al sabio que había robado, días antes, el camello predilecto del visir.Inútil es decir que Al-Hossein ignoraba aquel hurto audaz que preocupaba a todos y en torno del cual se habían hecho infructuosas pesquisas.
Descubierto, así, el autor del robo, el camello fue restituido pocas horas después a su poderoso dueño y el ladrón, amparado por el prestigio de Al-Hossein, se libró de severa sentencia, siendo perdonado [36].
¿Cómo explicar los motivos que llevaran al criminal a revelar su secreto? Lo sucedido era, sin embargo, muy sencillo: la figura geométrica hecha por el matemático para explicar la proposición de Euclides, era exactamente igual a la “marca” que tenía el camello robado. El ladrón, al ver la figura, creyó que Al-Hossein conocía su secreto y, lleno de indecible espanto, no se sintió con ánimo de ocultar la verdad.
La fama de Al-Hossein, desde ese día, se volvió, bajo el cielo de Persia, cien veces mayor.
¡No era para menos! ¡Con una simple figura geométrica descubrió al más audaz ladrón, y encontró un camello que ya se daba por perdido!
Capítulo 9
En el cual recibimos la visita del sheik Iezid. Extraña consecuencia de la previsión de un astrólogo. La mujer y la Matemática. Beremís es invitado a enseñar Matemática a una joven. Situación singular de la misteriosa alumna. Beremís habla de su antiguo maestro, el sabio No-Elin.
- ¿Algún nuevo problema que resolver? – preguntó Beremís.
- ¡Adivinó!... –respondió Iezid- . Me hallo en la necesidad de resolver un grave problema. Tengo una hija llamada Telassim [37], dotada de gran inteligencia y marcada de inclinación para los estudios. Cuando nació Telassim, consulté a un astrólogo famoso que sabía revelar el futuro por la observación de las nubes y las estrellas. Ese mago afirmó que mi hija viviría feliz hasta los 18 años; a partir de esa edad se vería amenazada por un cúmulo de desgracias lamentables. Había, no obstante, un medio de evitar que la desdicha cayese sobre ella. Telassim –añadió el mago- debía aprender las propiedades de los números y todas las operaciones que con ellos se hacen. Ahora bien: para dominar los números y hacer cálculos es necesario conocer la ciencia de Al-Carismi, es decir, la Matemática. Resolví, pues, asegurar a Telassim un futuro feliz haciendo que estudiase los misterios del Cálculo. Busqué varios “Ulemas” [38] de la Corte, mas no logré hallar uno solo que se sintiese capaz de enseñar Matemática a una joven de 17 años. Uno de ellos, dotado de gran talento, intentó disuadirme de tal propósito. Quien quisiese enseñar canto a una jirafa, cuyas cuerdas vocales no pueden producir el menor sonido, perdería el tiempo trabajando inútilmente. La jirafa, por su propia naturaleza, no podría cantar. Del mismo modo, el cerebro femenino (explicó el monje mahometano) es incompatible con las nociones más simples de Matemática. Se basa esa incomparable ciencia en el raciocinio, en el empleo de fórmulas y principios demostrables con los poderosos recursos de la Lógica y de las Proporciones. ¿Cómo podrá una pequeña, encerrada en el “harem” [39] de su padre, aprender fórmulas de Álgebra y teoremas de Geometría? ¡Nunca! Es más fácil que una ballena vaya a la Meca en peregrinación, que una mujer aprenda Matemática. ¿Para qué luchar contra lo imposible? ¡Mactub! [40]. Si la desgracia debe caer sobre nosotros, ¡que se haga la voluntad de Alah! El mayor de los desánimos se apoderó de mí al oír aquellas palabras. Sin embargo, yendo cierta vez a visitar a mi amigo Salen Nasair, el mercader, oí referencias elogiosas del nuevo calculista persa que llegara a Bagdad. Hablóme del episodio de los ocho panes, y ese caso, narrado minuciosamente, me impresionó. Procuré conocer al talentoso matemático y fui con ese fin a la casa del visir Maluf, quedando asombrado con la solución dada al problema de los 257 camellos reducidos luego a 256.
La Geometría, dijo Platón, existe en todas partes. En el disco del sol, en la forma del datilero, en el arco iris, en el diamante, en la estrella de mar, en la tela de la araña y hasta en un pequeño grano de arena. En la figura de arriba vemos la forma perfecta que presenta la flor del maracuyá. Es admirable la simetría pentagonal con que están dispuestos los elementos de esa flor. Llamamos la atención del lector para una observación realmente extraordinaria: “Las simetrías de orden impar sólo se encuentran en los seres dotados de vida. La materia inorgánica sólo presenta simetría par”
El jefe Iezid, irguiendo la cabeza, miró fija y solemnemente al calculista, y añadió:- ¿Será capaz, el hermano de los árabes, de enseñar los artificios del cálculo a mi hija Telassim? Pagaré por las lecciones el precio que me indique, pudiendo, como ahora, seguir en el cargo de secretario del visir Maluf.
- ¡Generoso sheik! –exclamó Beremís-. No encuentro motivo para rechazar vuestra invitación. En pocos meses podré enseñar a vuestra hija todas las operaciones algebraicas y el secreto de la Geometría. Se equivocan dos veces los filósofos cuando intentan medir con unidades negativas la capacidad intelectual de la mujer. La inteligencia femenina, cuando es bien orientada, puede acoger perfectamente las bellezas y secretos de la ciencia. Tarea fácil sería desmentir los conceptos injustos formulados por el sacerdote. Los historiadores citan varios ejemplos de mujeres que se hicieron célebres por su cultura matemática. En Alejandría, por ejemplo, vivió Hipatia, que enseñó la ciencia del cálculo a centenares de personas, comentó las obras de Diofanto, analizó los dificilísimos trabajos de Apolonio y rectificó todas las tablas astronómicas usadas hasta entonces. No hay motivo, oh sheik, para afligirse ni dudar. Vuestra hija aprenderá fácilmente la ciencia de Pitágoras. Deseo solamente que determinéis el día y hora en que deberá iniciar las lecciones.
Respondió el noble:
- Lo más de prisa posible. Telassim cumplió ya 17 años, y estoy ansioso por librarla de las tristes previsiones del astrólogo.
Y añadió:
- Debo advertirlo de una particularidad que no deja de tener importancia en este caso. Mi hija vive encerrada en el “harem” y nunca fue vista por hombres extraños a nuestra familia. Solo podrá, por lo tanto, oír sus lecciones de Matemática, oculta por una espesa cortina, con el rostro cubierto por un “jaique” y vigilada por dos esclavas de confianza. ¿Acepta, aún así, mi propuesta?
- Acepto con gran satisfacción –respondió Beremís-. Es evidente que el recato y pudor de una joven valen mucho más que los cálculos y las fórmulas algebraicas. Platón, filósofo y matemático, mandó colocar la leyenda siguiente en la puerta de su escuela:
“No entre si no es geómetra”.
Presentóse un día un joven de costumbres libertinas y manifestó deseos de frecuentar la academia. El maestro, sin embargo, no lo admitió, diciendo: “La Geometría es pureza y simplicidad; tu impudicia ofende a tan pura ciencia”. El célebre discípulo de Sócrates procuraba, de ese modo, demostrar que la Matemática no armoniza con la depravación y con las torpes indignidades de los espíritus inmorales. Serán, pues, encantadoras las lecciones dadas a esa joven que no conozco y cuyo rostro candoroso jamás tendré la ventura de admirar. Queriéndolo usted, podré iniciar mañana las lecciones.- Perfectamente –asintió el jefe-. Uno de mis siervos vendrá mañana a buscarlo (¡queriendo Alá!), poco después de la segunda oración. ¡Uassalam!
Después que el jefe Iezid dejó la posada, interrogué al calculista:
- Escucha, Beremís. Hay en todo eso un punto oscuro para mí. ¿Cómo podrás enseñar Matemática a una joven, cuando, en verdad, nunca estudiaste esa ciencia en los libros, ni tomaste lecciones de los “ulemas”? ¿Cómo aprendiste el cálculo, que aplicas con tanto brillo y oportunidad? Bien lo sé, calculista: entre pastores persas, contando ovejas, dátiles y bandadas de pájaros en vuelo por el cielo.
- Estás equivocado, “bagdalí” –replicó con serenidad el calculista-. En el tiempo en que vigilaba los rebaños de mi amo, en Persia, conocí a un viejo derviche llamado No-Elin, a quien, durante una tempestad de arena, salvé de la muerte. Desde ese día, el bondadoso anciano fue mi amigo. Era un gran sabio y me enseñó muchas cosas útiles y maravillosas. Fue con él que aprendí las reglas que permiten efectuar los cálculos con precisión y rapidez. El prudente derviche me decía: “la Matemática se funda únicamente en la verdad, sin tener en cuenta ninguna autoridad, tradición, interés o preconcepto. Lo mismo ocurre con cualquier ciencia, pero no de una manera tan clara como en la Matemática, pues, en mayor o menor grado, hay en las otras ciencias alguna cosa que se basa en la autoridad de los investigadores.” Me habló muchas veces de los grandes trabajos que los geómetras de la antigüedad habían realizado. Gracias al auxilio de ese derviche, llegaron a mi conocimiento las obras de Euclides, Thales, Pitágoras, del gran Arquímedes y de muchos otros sabios de la antigua Grecia.
Después de hacer una pequeña pausa, concluyó Beremís:
- No-Elin me enseñaba Matemáticas haciendo curiosas figuras en la arena o rayando, con la punta de una aguja, las hojas de una planta llamada “idomeg”[41]. Verás como podré enseñar Matemática lo mismo, sin ver el rostro de la que va a ser mi discípula.
Capítulo 10
En el cual vamos al palacio de Iezid. El rencoroso Tara-Tir no confía en el calculista. Los pájaros cautivos y los números perfectos. El “Hombre que calculaba” exalta la caridad del sheik. Oímos una tierna y arrebatadora canción .
Guiados por un amable y diligente criado, atravesamos de prisa las calles tortuosas del barrio Mouassan, yendo a dar un suntuoso palacio que se erguía en medio de un bello jardín.
Beremís quedó encantado con el aspecto artístico que el rico Iezid procuraba dar a su residencia. En el centro del parque levantábase una gran cúpula plateada, donde los rayos solares se deshacían en fulgores rutilantes. Un gran patio, por fuerte portón de hierro, ornamentado con todos los recursos del arte, daba entrada hacia el interior.
Un segundo patio interno, con un bien cuidado jardín en su centro, dividía el edificio en dos cuerpos. Uno de ellos estaba destinado a los aposentos particulares y el otro a las salas de reunión, así como a un comedor, en el cual el sheik cenaba, a veces, en compañía de poetas y escritores.
El aspecto exterior, a pesar de la artística ornamentación del vestíbulo, era triste y sombrío. Quien reparase en las ventanas enrejadas no podía sospechar la pompa y el arte con que todos los aposentos estaban decorados.
Una galería con lindas arcadas sostenidas por nueve o diez esbeltas y delgadas columnas de mármol blanco con arcos recortados elegantes capiteles, con las paredes revestidas de azulejos en relieve y el piso de mosaico, comunicaba los dos cuerpos del edificio; dos largas escalinatas, también de mármol, conducían al jardín, donde flores de diversas formas y perfumes bordeaban un tranquilo lago.
Un vivero lleno de pájaros, adornado con mosaicos y arabescos, parecía ser lo más importante del jardín. Había allí aves de exóticos cantos de variadas formas y rutilantes plumajes. Algunas, de peregrina belleza, pertenecían a especies para mí desconocidas.
Nos recibió el dueño de casa, con mucha simpatía, viniendo a nuestro encuentro en el jardín. Se hallaba en su compañía un joven moreno, delgado y de amplios hombros, que nos resultó simpático. Tenía un modo agresivo de mirar, y la forma en que hablaba era bastante desagradable, llegando, en ciertos momentos, hasta ser insolente.
- ¿Es pues, éste el calculista? –observó, subrayando las palabras con tono de menosprecio-. Me admira tu buena fe, querido Iezid. Vas a permitir que un mísero encantador de serpientes se aproxime y dirija la palabra a la encantadora Telassim. ¡No faltaba más! ¡Por Alah, que eres ingenuo!
Y pronunció una carcajada injuriosa.
Aquella grosería me sublevó. Tuve ímpetus de repeler la descortesía de aquel atrevido. Beremís, sin embargo, continuaba imperturbable. Era posible, tal vez, que el algebrista descubriera, en las palabras insultantes que oyera, nuevos elementos para hacer cálculos o para resolver problemas.
El poeta, mostrándose apenado por la actitud poco delicada de su amigo, dijo:
- Perdone, señor calculista, el juicio precipitado que acaba de hacer mi primo “el-hadj” Tara-Tir [42]. Él no conoce, ni puede evaluar su capacidad matemática, pues está por demás ocupado por el futuro de Telassim.
- No lo conozco, es claro; no me empeño mayormente en conocer los camellos que pasan por Bagdad en busca de sombra y alfalfa –replicó iracundo Tara-Tir, con insultante desprecio.
Y siguió hablando de prisa, nervioso y atropelladamente:
- Puedo probar, en pocos minutos, primo mío, que estás completamente engañado respecto a la capacidad de ese aventurero. Si me lo permites, yo lo confundiré con dos o tres simplezas que oí a un maestro de escuela en Mosul.
- Seguramente –convino Iezid-. Puedes interrogar a nuestro calculista y proponerle, ahora mismo, el problema que quisieras.
- ¿Problema? ¿Para qué? ¿Quieres confrontar a un chacal que aúlla con un “ulema” que estudia? –interrumpió groseramente-. Te aseguro que no será necesario inventar problemas para desenmascarar al “sufi” [43] ignorante. Llegaré al resultado que pretendo sin fatigar la memoria, más rápidamente de lo que piensas.
Y, apuntando hacia el gran criadero, interpretó a Beremís, fijando en nosotros sus pequeños ojos acerados, que brillaban inexorables:
- Respóndame, calculista del “Patito” [44], ¿cuántos pájaros hay en ese criadero?
Beremís Samir cruzó los brazos y se puso a observar con viva atención. Sería prueba de insana, pensé tratar de contar tantos pájaros, que inquietos volaban por todos lados, ya cruzándose en el aire, ya sustituyéndose en las perchas con increíble ligereza.
Al cabo de algunos minutos se volvió el calculista hacia el generoso Iezid y le dijo:
- Ruego a vos, jefe, mandéis soltar inmediatamente tres pájaros cautivos. Será de ese modo más fácil y agradable, para mí, enunciar el número total.
Aquel pedido tenía todo el aspecto de un disparate. Está claro que quien cuenta cierto número, podrá contar, fácilmente, ese número más 3.
Iezid, intrigadísimo, con el inesperado pedido del calculista, hizo comparecer al encargado del criadero y le dio órdenes para que la solicitud del calculista fuese atendida: libertados prontamente, tres lindos colibríes volaron rápidos por el cielo hacia fuera.
- Se encuentran ahora en el criadero –declaró Beremís- cuatrocientos noventa y seis pájaros.
- ¡Admirable! –exclamó Iezid entusiasmado-. Es así. Mi colección era de medio millar. Descontando los tres que ahora solté y un ruiseñor que envié a Mosul, quedan precisamente 496.
La suma de los divisores de 496, menores a 496 es:
| 1 | ||
| 2 | ||
4 | ||
| 8 | ||
| 16 | ||
| 31 | ||
| 62 | ||
| 124 | ||
| 248 |
- Acertó por casualidad –rezongó, lleno de rencor, el terrible Tara-Tir.
El poeta Iezid, instigado por la curiosidad, preguntó a Beremís:
- ¿Puede decirme, amigo mío, por qué prefirió contar 496, cuando es tan sencillo contar 496 + 3, o sea 499?
- Puedo explicarle, oh sheik, la razón de mi pedido –respondió Beremís con altivez-. Los matemáticos procuran siempre dar preferencia a los números notables y evitar los resultados inexpresivos o vulgares. Ahora bien: entre 499 y 496 no se puede dudar. El número 496 es un número perfecto y debe merecer nuestra preferencia.
- ¿Y qué es un número perfecto? –preguntó el poeta.
- Número perfecto –aclaró Beremís- es el que presenta la propiedad de ser igual a la suma de sus divisores, excluyéndose, claro está, el propio número. Así, por ejemplo, el número 28 presenta 5 divisores, menores que 28, son: 1, 2, 4, 7 y 14.
La suma de estos divisores,
1 + 2 + 4 + 7 + 14 = 28
por consiguiente, 28 pertenece a la categoría de los denominados números perfectos.El número 6, también lo es. Los divisores de 6 (menores que 6) son 1, 2 y 3, cuya suma es 6. Al lado de 6 y de 28 puede figurar 496, que es también, como ya dije, un número perfecto [45].
El rencoroso Tara-Tir, sin querer oír más explicaciones, se despidió del sheik Iezid y se retiró destilando rabia, por la gran derrota sufrida al pretender poner en evidencia la falta de habilidad del calculista.
- Ruégole señor calculista –dijo Iezid- que no se ofenda por las palabras de mi primo Tara-Tir. Tiene él, exaltado temperamento, y desde que asumió la dirección de las minas de sal en Al-Derid, se ha vuelto irascible y violento.
Comprendí que el inteligente Beremís no deseaba causar disgusto al sheik, cuando respondió lleno de bondad:
- Dada la gran variedad de temperamentos y caracteres, no nos es posible vivir en paz con el prójimo sin refrenar nuestra ira y cultivar la paciencia. Cuando me siento herido por la injuria, procuro seguir el sabio precepto de Salomón:
Quien de repente se enfurece, es tonto;
Quien es prudente, disimula el insulto.
- Estoy, sin embargo, muy agradecido al poderoso Tasra-Tir, y no le puedo guardar rencor, pues su turbulento primo me ofreció la oportunidad de hacer nueve actos de caridad.
- ¿Cómo?
- Cada vez que ponemos en libertad un pájaro cautivo –explicó el calculista- practicamos tres actos de caridad. El primero, para con la avecilla, restituyéndole la libertad que le había sido robada; el segundo, para con nuestra conciencia, y el tercero, para con Dios.
- Quiere decir, entonces, que si diera libertad a todos los pájaros del criadero…
- Yo os aseguro, oh sheik, que practicando mil cuatrocientos ochenta y ocho actos de caridad –replicó prontamente Beremís, como si ya supiese de antemano el producto de 496 por 3.
Impresionado por estas palabras, el generoso Iezid ordenó que fueran puestas en libertad todas las aves que se hallaban en el criadero.
Los siervos y esclavos quedaron aterrados al oír esa orden. La colección, formada con paciencia y trabajo, valía una fortuna. En ella figuraban perdices, colibríes, faisanes multicolores, gaviotas negras, patos de Madagascar, lechuzas del Cáucaso, y varias golondrinas rarísimas de China y de la India.
- ¡Suelten los pájaros! –ordenó nuevamente el sheik, agitando la mano resplandeciente de anillos.
Las grandes puertas de tela metálica se abrieron. En grupos, de a pares, los cautivos dejaban la prisión y esparcíanse por la arboleda del jardín.
Dijo entonces Beremís:
- Cada ave, con las alas extendidas, es un libro de dos hojas abierto en el cielo. Es un gran crimen robar o destruir esa pequeña biblioteca de Dios.
En ese momento oímos el comienzo de una canción; la voz era tan tierna y suave, que se confundía con el trino de las golondrinas y el arrullar de las palomas.
Al principio era una melodía afable y triste, llena de melancolía y recuerdo, como las endechas de un ruiseñor solitario; animóse, luego, en un crescendo vivo, en gorjeos complicados, en trinos argentinos, entrecortados con gritos de amor que contrastaban con la serenidad de la tarde, y revoloteaban por el espacio como si fueran hojas que llevara el viento. Por último volvió al tono triste del principio, lanzando una nota desgarradora que quedó flotando en la límpida atmósfera, como un suspiro de virazón:
Si yo hablase las lenguas de los hombresEl encanto de aquella voz parecía envolver la tierra en una ola de indefinible alegría. El día parecía más claro, el cielo más azul y el aire más leve.
y de los ángeles y no tuviese caridad,
sería como el metal que suena,
o como la campana que tañe,
¡Nada sería!... ¡Nada sería!...
Si yo tuviese el don de la profecía y toda la ciencia,
de tal manera que transportase los montes,
y no tuviese caridad.
¡Nada sería!... ¡Nada sería!...
Si distribuyese todos mis bienes para el sustento
de los pobres
y entregase mi cuerpo para ser quemado,
y no tuviese caridad.
¡Nada sería!... ¡Nada sería!...
- Es Telassim que canta –explicó el jefe al reparar en la atención con que oíamos embebidos la extraña canción.
La bandada de pájaros que revoloteaba llenaba el espacio con sus alegres notas de libertad. No eran más que 496, pero daban la impresión de que eran ¡diez mil!...
- ¿Y de quién son esos brillantísimos versos? [46] –indagué.
- No lo sé. Una esclava cristiana los enseñó a Telassim y ella jamás los olvidó. Deben ser de algún poeta nazareno [47].
Subimos, y así se inició la primera lección de Matemática.
Capítulo 11
Beremís inicia su curso de Matemática. El número y el universo. Una frase de Platón. La unidad y Dios. Que medir. Las partes que forman la Matemática. La Aritmética y los números. El Álgebra y las relaciones. La Geometría y las formas. La Mecánica y la Astronomía. Un sueño del rey Aldebazan. La “alumna invisible” eleva a Alah una oración.
Adornaban las paredes caprichosos arabescos azules entrelazados con hermosos versos de Antar [48], el poeta del desierto. En el centro, entre dos columnas, con letras de oro sobre fondo azul, se leía este notable dístico:
“Cuando Alah quiere bien a uno de sus servidores
abre para él las puertas de la inspiración.”
La tarde declinaba; en el aire flotaba un suave perfume de incienso y rosas.
Las ventanas, de pulido mármol, estaban abiertas, dejando ver el jardín y los frondosos pomares, que se extendían hasta el parduzco y triste río.
Una esclava morena, de clásica hermosura circasiana, estaba de pié, el rostro descubierto, junto a la puerta.
- ¿Vuestra hija se halla ya presente? –preguntó Beremís al sheik.
- Seguramente -respondió Iezid-. Le ordené estar en el otro extremo de la habitación, detrás de la cortina, desde donde podrá ver y oír, permaneciendo sí invisible para los que aquí se hallen.
Realmente, las cosas fueron dispuestas de tal manera, que ni siquiera se distinguía la sombra de la joven que iba a ser discípula de Beremís. Era muy probable que ella nos estuviera observando por algún pequeño orificio hecho en el terciopelo, e imperceptible para nosotros.
- Pienso que es oportuno comenzar ya la primera lección –advirtió el sheik.
Y preguntó con cariño:
- ¿Estás atenta, Telassim, hija mía?
- Sí, padre -respondió una voz femenina de agradable timbre, desde el otro lado del aposento.
Mientras tanto Beremís se había preparado para la lección; cruzó las piernas, sentándose sobre un almohadón, en el centro de la sala. Yo procuré ser discreto, colocándome a un lado; junto a mí vino a sentarse el sheik Iezid.
Toda investigación científica, es costumbre que sea precedida por una oración. Fue, pues, así, que Beremís comenzó:
- Nosotros Te Adoramos, Señor, e imploramos Tu divina providencia. Condúcenos por el camino de la verdad; por el camino de los iluminados y bienamados por Ti.
Terminada la oración, así habló:
- Cuando miramos, señora, hacia el cielo, en las noches límpidas y calmas, sentimos que nuestra inteligencia es pequeña para concebir las obras maravillosas del Creador. Delante de nuestra mirada sorprendida, las estrellas son una caravana luminosa que desfila por el desierto insondable del infinito; las nebulosas inmensas y los planetas giran según leyes eternas por los abismos del espacio. Una noción surge, entretanto, bien nítida, en nuestro espíritu: la noción de número.
Vivió otrora, en Grecia, cuando ese país era dominado por el paganismo, un filósofo notable llamado Platón. (Alah es, sin embargo, más sabio). Consultado por un discípulo sobre las fuerzas dominantes de los destinos del hombre, el gran sabio respondió: “Los números gobiernan el mundo ”.
Realmente es así. El pensamiento más simple no puede ser formulado sin que en él se involucre, bajo múltiples aspectos, el concepto fundamental de número. El beduino que en medio del desierto, en el momento de la oración, murmura el nombre de Dios, tiene su espíritu dominado por un número: ¡La Unidad! Sí; Dios, según las verdades escritas en el Libro Santo y repetidas por el Profeta, es Uno, eterno e inmutable. Luego, el número Uno aparece en el cuadro de nuestra inteligencia como el símbolo del propio Creador.
Del número, señora, que es la base de la razón y del entendimiento, surge otra noción de indiscutible importancia: la noción de medida.
Medir, señora, es comparar. Por lo tanto, solo son susceptibles de medirse las magnitudes que admiten un elemento como base de comparación. ¿Será posible medir la extensión del espacio? De ningún modo. El espacio es infinito y, siendo así, no admite término de comparación. ¿Será posible avaluar la eternidad? De ninguna manera. Dentro de las posibilidades humanas, el tiempo es siempre finito, y en el cálculo de la Eternidad no puede lo efímero servir de unidad de evaluación.
En muchos casos, sin embargo, nos es posible representar una magnitud que no se adapte a los sistemas de medida, por otra que pueda ser avaluada con exactitud. Ese cambio de magnitudes, tendiente a simplificar los procesos de medidas, constituye el objeto principal de una ciencia, que los hombres denominan Matemática. Para alcanzar su objetivo, precisa la Matemática estudiar los números, sus propiedades y transformaciones. En esa parte ella toma el nombre de Aritmética. Conocidos los números, es posible aplicarlos a la evaluación de magnitudes que varían, o que son desconocidas, pero que se presentan expresadas por medio de relaciones y fórmulas. Tenemos así el Álgebra. Los valores que medimos en el campo de la realidad son representados por cuerpos materiales o por símbolos; en cualquier caso, esos cuerpos o esos símbolos están dotados por tres atributos: forma, tamaño y posición. Es necesario, pues, estudiar estos tres atributos; ese estudio constituye el objeto de la Geometría.
Estudia, además, la Matemática, las leyes que rigen los movimientos y las fuerzas, leyes que aparecen en la admirable ciencia que se denomina Mecánica.
La Matemática pone todos sus recursos al servicio de una ciencia que eleva el alma y engrandece al hombre. Esa ciencia es la Astronomía.
Hablan algunos de las Ciencias Matemáticas, como si la Aritmética, el Álgebra y la Geometría fuesen partes enteramente distintas. No es así, sin embargo. Todas se auxilian mutuamente, apoyándose unas en las otras, y, en ciertos puntos, se confunden.
Hay una ciencia única, la Matemática, la cual nadie se puede jactar de conocer, porque sus conocimientos son, por su naturaleza, infinitos, y de la cual todos hablan, sobre todo los que más la ignoran.
Entre los hombres que la estudian y la conocen hay, sin embargo, algunos que más se fijan en minucias que en las ideas generales, siendo, por lo tanto, sus descubrimientos de escasa importancia.
Nárrase que Moisés se encontró, cierta vez, en las playas de Judea, con El-Quíder[49], el más grande entre los sabios de la Tierra. Se hallaban los dos grandes Maestros conversando sobre los más altos problemas de la Vida y del Destino, cuando se acercó a ellos un pajarito que traía en el pico una gota de agua de mar. La pequeña avecilla, sin interrumpir el vuelo, dejó caer la gota sobre el hombro de El-Quíder. Él, que era sabio entre los sabios, dijo entonces a Moisés:
“¡Profeta de Dios! Ese pájaro acaba de enseñarnos una profunda verdad, mostrándonos de una manera elocuente, que la ciencia de Moisés, que es incalculable, acrecentada con paciencia de El-Quíder, que es bien poca, y la de todos los sabios de la Tierra –delante de la ciencia de Dios- es como una gota de agua comparada con el mar.”
La Matemática, señora, enseña al hombre a ser sencillo y modesto; es la base de todas las ciencias y todas las artes. Aldebazan, rey de Irak, descansando cierta vez en la galería de su palacio, soñó que encontraba siete jóvenes que caminaban por una ruta. En cierto momento, vencidas por la fatiga y por la sed, las jóvenes se detuvieron bajo el sol calcinante del desierto. Apareció, entonces, una hermosa princesa que se aproximó a las peregrinas, trayéndoles un gran cántaro de agua pura y fresca. La bondadosa princesa sació la sed que devoraba a las jóvenes, y éstas pudieron reanudar su interrumpida jornada.
Al despertar, impresionado con ese curioso sueño, decidió Aldebazan entrevistarse con un astrólogo famoso, llamado Sanib, a cual consultó sobre el significado de aquella escena en la que él –rey poderoso y justo- asistiera en el mundo de las visiones y fantasías. Dijo Sanib, el astrólogo “¡Señor! Las siete jóvenes que caminaban por la ruta, eran las artes divinas y las ciencias humanas: la Pintura, la Música, la Escultura; la Arquitectura, la Retórica, la Dialéctica y la Filosofía. La princesa que las socorrió representa la grande y prodigiosa Matemática. Sin el auxilio de la Matemática –prosiguió el sabio- las artes no pueden progresar, y todas las otras ciencias perecen.” Impresionado el rey por lo que oía, determinó que se organizasen en todas las ciudades, oasis y aldeas de su país, centros de estudios matemáticos. Elocuentes y hábiles “ulemas”, iban por orden del soberano recorriendo los bazares y caravanas, enseñando Aritmética a los caballeros y beduinos. En las paredes de las mezquitas y en las puertas de los palacios, los versos de los poetas famosos fueron sustituidos por fórmulas algebraicas y por cálculos numéricos.
Al cabo de pocos meses aconteció que el país atravesaba por una era de prosperidad. Paralelamente al progreso de la ciencia, crecían los recursos naturales del país, las escuelas estaban repletas; el comercio se acrecentaba en forma prodigiosa; multiplicábanse las obras de arte; levantábanse monumentos, y las ciudades estaban colmadas de turistas y curiosos. El país de Irak tenía abiertas las puertas al Progreso y a la Riqueza, si no hubiese la fatalidad, (¡Mactub!) puesto el término a aquel período de trabajo y prosperidad. El rey Aldebazan, acometido por repentina enfermedad, murió, siendo llevado por el maligno Azrail [50] para el cielo de Alah. La muerte del soberano abrió dos tumbas. Una de ellas acogió el cuerpo del glorioso Monarca, y la otra la cultura científica del pueblo. Subió al trono un príncipe vanidoso, indolente y de limitadas dotes intelectuales. Le preocupaban más las diversiones que los problemas Administrativos del Estado. Pocos meses después, todos los servicios públicos estaban desorganizados; las escuelas cerradas, y los artistas y “ulemas”, forzados huir bajo la amenaza de los malvados y ladrones. El tesoro público fue dilapidado en múltiples festines y desenfrenados banquetes. El país de Irak, llevado a la ruina por el desorden, fue atacado por enemigos ambiciosos, y vencido.
La historia de Aldebazan, señora, nos demuestra que el progreso de un pueblo se halla ligado al desenvolvimiento de los estudios matemáticos [51]. En el Universo todo es número y medida. La Unidad, símbolo del Creador, es el principio de todas las cosas, las cuales no existen sino en virtud de inmutables proporciones y relaciones numéricas. Todos los grandes enigmas de la Vida pueden ser reducidos a simples combinaciones de elementos variables o constantes, conocidos o desconocidos.
Para que podamos conocer la Ciencia es necesario tomar un número por fase. Veremos cómo estudiarlo con la ayuda de Alah, Clemente y Misericordioso.
- ¡Uaasalam!
Con estas palabras concluyó el calculista, dando por terminada su primera clase de Matemática.
Con agradable sorpresa oímos, entonces a la alumna, a quien hacía invisible la cortina, pronunciar la siguiente oración:
“¡Oh Dios Omnipotente, Creador del Cielo y de la Tierra! Perdona la pobreza, pequeñez y puerilidad de nuestros corazones. No escuches nuestros pedidos, pero oye el clamor de nuestras necesidades; no atiendas nuestros pedidos, pero ten en cuenta nuestros silenciosos gemidos. ¡Cuántas veces pedimos aquello que tuvimos y que dejamos perder! ¡Cuántas veces soñamos poseer aquello que nunca será nuestro! ¡Oh Dios! Nosotros te agradecemos por este Universo, que es nuestro grande hogar, por su vastedad y riqueza, y por la vida multiforme que en él existe y de la cual formamos parte. Loámoste por el esplendor del cielo azul y por la brisa de la tarde, por las veloces nubes y por las constelaciones de las alturas. Loámoste por los océanos inmensos, por el agua que corre, por las montañas eternas, por los árboles frondosos, por el suave césped en que reposan nuestros pies. ¡Nosotros te agradecemos los múltiples encantos con que podemos experimentar en nuestras almas las bellezas de la Vida y el Amor! ¡Oh Dios, Clemente y Misericordioso! Perdona la pobreza, la pequeñez y la puerilidad de nuestros corazones.”
Capítulo 12
En el cual veo a Beremís interesado en el juego de saltar con cuerda. La curva del “baq-taque” y las arañas. Pitágoras y el círculo. Encontramos a Harid Namur. El problema de los 60 melones. Cómo perdió el intendente la apuesta. La voz del muezín ciego llama a los creyentes para la oración de “mogreb”.
- Es, con seguridad, uno de los libertos de hoy –observé-. Reconforta oírlos traducir en melódicos cantos, la alegría de la libertad reconquistada.
Beremís, sin embargo, en aquel momento nos se preocupaba por el canto del pájaro. Absorbía su atención un grupo de pequeños que se divertían en la calle, a corta distancia. Dos de ellos sostenían, por los extremos, un trozo de cuerda fina que debía tener catorce o quince palmos de extensión. Los otros trataban de trasponer de un salto, la cuerda, colocada más o menos alta, conforme a la agilidad del saltador.
- Mira la cuerda, “bagdalí” –dijo el calculista, tomándome por el brazo-, ¡Observa qué curva perfecta! ¿No la hallas digna de estudio?
- Pues, amigo mío –dijo Beremís-: convéncete de que tus ojos son ciegos para las más grandes bellezas y maravillas de la Naturaleza. Cuando los niños tienen la cuerda, sosteniéndola por los extremos, dejándola caer libremente y bajo su propio peso, la cuerda forma una curva notable, pues surge como resultante de fuerzas naturales [52]. Yo tuve ocasión de observar esa curva –que el sabio No-Elin llamaba la “baq-taque” [53], porque tiene la forma de la joroba de ciertos dromedarios-. ¿Tendrá esa curva plana alguna analogía con las derivadas de la parábola? En lo futuro, si Alah lo quiere, los matemáticos descubrirán el medio de trazar esa curva, punto por punto, y estudiarán rigurosamente todas sus propiedades.
- Hay, sin embargo –prosiguió-, muchas otras curvas más importantes. Debo citar, en primer lugar, el círculo [54]. Pitágoras, filósofo y matemático, consideraba al círculo como la figura más perfecta, relacionándolo así con la idea de perfección. Entre todas las curvas más perfectas, el círculo es la que tiene el trazado más simple.
Beremís, interrumpiendo en ese momento la disertación apenas comenzada sobre las curvas, señaló hacia un jovencito que se hallaba a corta distancia y gritó:
- ¡Harim Namir!
El joven se volvió rápidamente y vino alegre a nuestro encuentro. Me di cuenta entonces, que se trataba de uno de los tres hermanos que habíamos visto discutir en el desierto, cierto día, por causa de la herencia de los 35 camellos; reparto complicado, lleno de tercios y novenos, que Beremís resolvió por medio de un artificio curioso, al que ya me he referido.
- ¡Mac Alah! – exclamó Harim, dirigiéndose a Beremís-. Ha sido el Destino quien dispuso ahora nuestro encuentro. Mi hermano Hamed se halla atribulado por una cuenta de 60 melones que nadie puede resolver.
Y Harim nos llevó a una pequeña casa en donde se encontraba su hermano Hamed Namur, en compañía de varios mercaderes.
Mostróse Hamed muy satisfecho al ver a Beremís y, volviéndose hacia los mercaderes, les dijo:
- Este hombre que acaba de llegar, es un gran matemático. Gracias a su valiosa ayuda pusimos hallar la solución perfecta de un problema que nos parecía imposible: dividir 35 camellos entre 3 personas. Estoy seguro de que él podrá explicar, en pocos minutos, la diferencia encontrada en la venta de los 60 melones.
Como era necesario informar minuciosamente a Beremís, uno de los mercaderes tomó la palabra y dijo:
- Los dos hermanos, Harim y Named, me encargaron vender en el mercado dos partidas de melones. Harim me entregó 30 melones, que debían ser vendidos á razón de 3 por un denario; Hamed me dio, también, 30 melones, para los cuales fijó un precio más elevado, esto es, a razón de dos por un denario. Era bien claro que, terminada la venta, Harim recibiría 10 y su hermano 15 denarios. El total obtenido sería, pues, de 25 denarios. Sin embargo, al llegar a la feria, una duda me acometió: Si yo vendo primero los melones caros, pensé, peco de imparcialidad, y si vendo los más baratos primero, encontraré dificultad para colocar los otros. Lo mejor será que venda las dos partidas, al mismo tiempo. Habiéndose llegado a esa conclusión, reuní los 60 melones y comencé a venderlos a 5 por 2 denarios. El negocio se justificaba con un simple razonamiento. Si debía vender 3 por un denario y luego 2 por la misma suma, era más simple que vender 5 por 2 denarios. Vendidos los 60 melones en 12 lotes de 5 cada uno obtuve 24 denarios. ¿Cómo pagar a los dos hermanos, si uno debía recibir 10 y el otro 15 denarios? Había una diferencia de un denario, que no sabía cómo explicar, pues el negocio había sido hecho con todo cuidado. Vender 3 por un denario y 2 por 1, ¿no es lo mismo que vender 5 por 2 denarios?
- La cuestión no tendría importancia alguna –intervino Hamed Namir- si no fuese por la intervención absurda del “vequil” [55] que vigila la feria. Habiendo oído algo sobre el caso, y no sabiendo explicar la diferencia, ha apostado 5 denarios a que esa diferencia provenía de la falta de un melón que fuera robado durante la venta.
- El “vequil” no tiene razón –afirmó Beremís- y debe ser obligado a pagar la apuesta. La diferencia que encontró el vendedor se debe a lo siguiente: La partida de Harim se componía de 10 lotes de 3 melones cada uno. Cada lote debía ser vendido a un denario. El total de la venta sería 10 denarios. La partida de Hamed se componía de 15 lotes (con dos melones cada uno) y un total de 15 denarios. Observen que el número de lotes de una partida es diferente al de la otra. Para vender los melones en lotes de 5 cada uno, sólo los 10 primeros lotes podrían ser vendidos (sin perjuicio) por 2 denarios cada uno. Vendidos esos 10 lotes, quedan todavía 10 melones, que pertenecen exclusivamente a la partida de Hamed y que, siendo de precio más elevado, debían ser vendidos a razón de 2 por 1 denario. La diferencia de un denario resultó, pues, de la venta de los 10 últimos melones. No hubo robo alguno. De la desigualdad de los precios e las dos partidas, resultó la pérdida de un denario, que se verificó en el resultado final.
En esta figura que aclara el problema de los 60 melones. En A están representados los 30 melones que debían ser vendidos a razón de 3 por 1 denario; en B los 30 más caros, cuyo precio era de 2 por un denario. Como el dibujo nos muestra, sólo hay 10 lotes de 5 cada uno (siendo 3 de A, y 2 de B) que pueden ser vendidos sin perjuicio a razón de 2 denarios cada uno. En ese momento la voz del “muecín”, cuyo eco vibraba en el aire al llamar a los fieles para la oración, interrumpió nuestra reunión.
- ¡Hai al el-salah![56] ¡Hai al el-salah!
Cada uno de nosotros procuró, sin pérdida de tiempo, hacer, según lo indica el Libro Santo, las “guci” de ritual.
El Sol ya se hallaba sobre la línea del horizonte. Había llegado la hora del “mogreb”.
Desde la tercera almenara [57] de la mezquita de Omar, el “muecín” ciego llamaba, con voz pausada y ronca, a los creyentes para la oración:
- Alah es grande y Mahoma es el verdadero enviado de Dios. ¡Venid a orar, musulmanes! ¡Venid a orar!
Los mercaderes, precedidos por Beremís, extendieron sus tapetes de colores, se sacaron las sandalias, miraron la dirección de la Ciudad Santa y exclamaron:
- ¡Alah, omnipotente y misericordioso! Loado sea el Creador de los mundos visibles e invisibles. A ti, que eres el verdadero Sol del mundo; que siempre alumbras, sin tener ocaso; que con tus rayos benéficos y con tu luz, alegras y avivas todas las cosas en el Cielo y en la Tierra: Te rogamos que misericordiosamente brilles en nuestros corazones, para que la noche y la oscuridad del pecado, y la niebla del error, sean disipadas por el brillo de Tu luz en nuestros corazones, y nosotros por toda nuestra vida andemos sin tropezar, como de día, puros, alcanzando las bendiciones abundantes que tienes para nosotros.
Capítulo 13
En el cual vamos al palacio del califa. Beremís es recibido por el rey. Los poetas y la Amistad. La amistad entre los hombres y la amistad entre los números. Números amigos. El califa elogia al “Hombre que calculaba”. Es exigida en palacio, la presencia de un calígrafo.
Aquella comunicación, tan grata para cualquier musulmán, fue recibida por Beremís y por mí con verdadera ansiedad.
Era muy posible que el soberano, al oír al sheik Iezid contar alguna de las proezas practicadas por el eximio matemático, tuviese curiosidad por conocer al “Hombre que calculaba”. No se puede explicar de otra forma nuestra presencia en la Corte, entre las figuras de más prestigio de la alta sociedad de Bagdad.
Quedé asombrado al entrar en el palacio del Emir.
Varias arcadas superpuestas, formando curvas armoniosas, y sostenidas por altas y delgadas columnas esculpidas, tenían sus basamentos ornados con finísimos mosaicos. Pude notar que esos mosaicos estaban formados por fragmentos de loza blanca y bermeja, alternando con franjas de estuque.
Los techos de los salones principales eran de color oro y azul; las paredes de todas las habitaciones se presentaban cubiertas de azulejos en relieve, y los pisos eran de mosaico.
Las cortinas, los tapices, los divanes, todo, en fin, cuanto constituía el mobiliario del palacio, demostraba la magnificencia indiscutible de un príncipe de leyenda hindú.
Afuera, en los jardines, se notaba la misma pompa, realzada por la mano de la Naturaleza, perfumada por mil aromas diferentes, alfombrada con verde césped, bañada por el río, refrescada por innumerables fuentes de mármol blanco, junto a las cuales un millar de esclavas trabajaban sin cesar.
Fuimos conducidos por un ayudante del visir Ibraim Maluf hasta la Sala de las Audiencias.
Vimos al llegar, al poderoso monarca sentado en riquísimo trono de marfil y terciopelo.
Perturbóme algo la belleza sublime del salón. Todas sus paredes estaban adornadas con inscripciones admirables, hechas por el arte caprichoso de algún calígrafo genial. Las leyendas aparecían, en relieve, sobre fondo azul claro con letra pequeña y roja. Casi todas eran versos de los poetas más famosos de nuestra patria. Jarrones con flores por todas partes, flores deshojadas sobre los cojines, sobre las alfombras, o en bandejas de oro y plata primorosamente cinceladas.
Hermosas y numerosas columnas lucían, airosas, con sus capiteles y basamentos, elegantemente ornadas por el cincel de artistas árabes, que sabían, como ninguno, multiplicar ingeniosamente las figuras geométricas asociadas con flores y hojas de tulipán, azucenas y mil diversas plantas, en una armonía maravillosa de inenarrable belleza.
Se hallaban presentes siete visires, dos jueces, varios doctores y diversos dignatarios de gran prestigio.
Al honrado Maluf correspondía hacer nuestra presentación. En el desempeño de esta misión, el visir, con los codos apoyados en la cintura y las palmas de las manos hacia fuera, habló así:
- Para satisfacer tu deseo, rey del tiempo, ordené compareciesen hoy, a esta excelsa audiencia, el calculista Beremís Samir, mi actual secretario, y su amigo Hank-Tade_Madya, auxiliar de escribiente y funcionario de palacio.
- Sean bienvenidos, musulmanes. –respondió con sencillez el sultán-. Admiro a los sabios. Un matemático, bajo el cielo de este país, contará siempre con mi simpatía y, si fuera necesario, con mi decidida protección.
- ¡Alah badie, ya sidi![58] –exclamó Beremís, inclinándose delante del rey y besando, respetuoso, la tierra entre las manos[59].
Quedé inmóvil, la cabeza inclinada, los brazos cruzados, pues no habiendo sido aludido en los elogios por el soberano, no podía tener el honor de dirigirle el “zalam”.
El hombre que tenía en sus manos el destino del pueblo árabe parecía bondadoso y desprovisto de prejuicios. Tenía el rostro delgado, quemado por el sol del desierto y surcado de arrugas prematuras. Vestía con relativa sencillez. Llevaba en la cintura, bajo la faja de seda, un hermoso puñal, cuyo cabo estaba adornado con piedras preciosas. El turbante era verde con pequeñas listas blancas. El color verde es –como todos saben- lo que distingue a los descendientes de Mahoma, el Santo Profeta (¡con Él haya paz y gloria!).
- Muchas cosas importantes quiero resolver en la audiencia de hoy –comenzó el califa-. No quiero, sin embargo, iniciar los trabajos y discutir los grandes problemas políticos, sin recibir una prueba clara y precisa que el matemático persa recomendado por mi amigo Iezid es, realmente, un gran y hábil calculista.
Interpelado de ese modo Beremís por el glorioso monarca, se sintió obligado a corresponder brillantemente a la confianza que el jefe Iezid, en él depositara.
Dirigiéndose, pues, al sultán, así le habló:
- No soy más, Comendador de los Creyentes, que un rudo pastor que acaba de ser distinguido con vuestra honrosa atención.
Y después de corta pausa prosiguió:
- Aseguran, entretanto, mis generosos amigos, que es justo incluir mi nombre entre los calculistas. Siéntome halagado por tan alta distinción, aunque pienso que, en general, los hombres son buenos calculistas. Calculista es el pescador que cuenta los peces que hay en su red; calculista es el soldado que avalora de una ojeada, cuando está en campaña, la distancia de una parasanga; el calculista es el poeta que cuenta las sílabas y mide el ritmo de los versos; calculista es el músico que aplica, en la división en compases, las leyes de la perfecta armonía; calculista es el pintor que traza las figuras según proporciones invariables, para obtener perspectiva; calculista es el humilde tejedor que dispone uno por uno, todos los hilos de su trabajo. ¡Todos, en fin, oh rey, son buenos y hábiles calculistas!
Y, después de mirar a todos los nobles que rodeaban el trono, Beremís prosiguió:
- Veo, con infinita alegría, que estáis rodeado de “ulemas”, y doctores; que hay, a la sombra de vuestro trono poderoso, hombres de valor que cultivan el estudio y engrandecen la ciencia. La compañía de los sabios, oh rey, es para mí el mayor tesoro. El hombre sólo vale por lo que sabe. Saber es poder. Los sabios educan por el ejemplo, y nada hay que conquiste al espíritu humano más profundamente que el ejemplo. Sin embargo, no debe el hombre cultivar la ciencia si no es para utilizarla en la práctica del bien. Sócrates, filósofo griego, afirmaba con el peso de su autoridad enorme: “Sólo es útil el conocimiento que nos hace mejores”. Séneca, otro pensador famoso, decía, incrédulo: “¿Qué importa saber que es una línea recta, si no se sabe lo que es la rectitud?” Permitidme, pues, rey generoso y justo, que rinda mi humilde homenaje a los doctores y “ulemas” que se hallan en esta sala.
Durante los trabajos diarios, observando las cosas que Alah sacó de la Nada para darles vida, aprendí a valorar los números y a transformarlos por medio de reglas prácticas y seguras. No deja de preocuparme, sin embargo, la prueba que solicitáis. Confiado en vuestra proverbial generosidad, agrádame decir que observo en esta Sala de Audiencias, demostraciones admirables y elocuentes de que la Matemática existe en todas partes. Adornan las paredes de este bello salón varios versos que contienen un total de 504 palabras, estando algunas trazadas en caracteres negros y las restantes en rojo. El calígrafo que dibujó estos versos demostró tener tanto talento e imaginación al descomponer las 504 palabras, como los poetas que escribieran esas inmortales poesías.
¡Rey magnánimo! –prosiguió Beremís-: encuentro en los versos incomparables que adornan esta Sala de Audiencias grandes elogios sobre la Amistad. Puedo leer allí, cerca de la columna, la célebre “cassida” de “Mohalhil”:
“Si mis amigos me huyeran, de mí huirían todos los tesoros.”
Un poco más abajo encuentro el elocuente pensamiento de Tarafa:
“El encanto de la vida depende únicamente de las buenas amistades que cultivamos.”
A la izquierda se destaca el profundo concepto de Hatim, de la tribu de Tai:
“La buena amistad es para el hombre lo que el agua pura y límpida para el beduino sediento.”
Sí, todo eso es sublime, profundo y elocuente. La mayor belleza, sin embargo, reside en el ingenioso artificio empleado por el calígrafo para demostrar que la amistad que los versos exaltan, no existe solamente entre los seres dotados de vida y sentimientos. La amistad se halla, también entre los números.
¿Cómo descubrir –preguntaréis- entre los números, aquellos que están unidos por los lazos de la amistad matemática? ¿De qué medios se vale el geómetra para señalar en la serie numérica los elementos ligados por la estima?
En pocas palabras podré explicar en qué consiste el concepto de los números amigos en Matemática.
Consideremos, por ejemplo, los números 220 y 284.
El número 220 es divisible exactamente por los números:
1, 2, 4, 5, 10, 11, 20, 22, 44, 55 y 110.
Estos son los divisores de 220 menores que 220 y su suma:1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284
El número 284 es –a su vez- divisible exactamente por los números:1, 2, 4, 71 y 142.
Son esos los divisores de 284 menores que 284 y su suma:1 + 2 + 4 + 71 + 142 = 220
Pues bien. Hay entre esos números relaciones notables. Si sumamos los divisores de 220, arriba indicados, obtenemos una suma igual á 284; si sumamos los divisores de 284, el resultado es, precisamente, 220.De esa relación los matemáticos llegaron a la conclusión de que los números 220 y 284 son “amigos”; es decir, que cada uno de ellos parece existir para servir, alegrar, defender u honrar al otro.
Y el calculista concluyó:
- ¡Pues bien, rey generoso y justo! Observad que las 504 palabras que forman el elogio poético de la Amistad fueron escritas en la siguiente forma:
220 en caracteres negros y 284 en caracteres rojos. Y 220 y 284 son, como ya expliqué, números amigos.
Observad, también, una relación no menos interesante: las 504 palabras forman 32 leyendas diferentes. Pues bien, la diferencia entre 284 y 220 es 64, número que, además de ser cuadrado y cubo perfecto, es precisamente igual al doble del número de leyendas dibujadas.
El infiel dirá que se trata de simples coincidencias. Sin embargo, aquel que cree en Dios y tiene la dicha de seguir las enseñanzas del Santo Profeta Mahoma (¡con Él en la oración y en la paz!), saben que las llamadas coincidencias no serían posibles si Alah no las describiese en el libro del Destino. Afirmo, pues, que el calígrafo, al descomponer el número 504 en dos porciones (220 y 284), escribió sobre la Amistad un poema que eleva a todos los hombres de alma noble y espíritu claro.
Al oír las palabras del calculista, el califa quedó extasiado. Resultaba extraordinario. Resultaba extraordinario que aquel hombre contase, de una mirada, las 504 palabras de los 32 versos y que, al contarlas, verificase que había 220 en negro y 284 en letras rojas.
- Tus palabras, calculista –dijo el rey- me han dado la certeza de que eres un geómetra de gran mérito. He quedado encantado con esa interesante relación que los algebristas denominan “amistad numérica”, y estoy ahora interesado en saber cuál fue el calígrafo que escribió, al hacer el decorado de esta habitación, los versos que sirven de adorno a estas paredes.
Es fácil verificar si la descomposición de las 504 palabras, en partes que formen números amigos, fue hecha a propósito o resultó de un capricho del Destino (obra exclusiva de Alah, el Exaltado).
Y haciendo aproximar al trono a uno de sus secretarios, el sultán Al Motacen le preguntó:
- ¿Recuerdas Nuredín Zarur, al calígrafo que trabajó en este palacio?
- Lo conozco muy bien –respondió prontamente el sheik-. Vive junto a la mezquita de Otman.
- Traedlo aquí, “sejid”[60] , lo más pronto posible –ordenó el califa-. Quiero interrogarlo.
- ¡Escucho y obedezco!
Y salió a prisa a cumplir la orden del soberano.
Capítulo 14
En el cual esperamos en el trono real, el regreso de Nuredín Zarur, el emisario del califa. Los músicos y las bailarinas gemelas. Como Beremís reconoció a Iclimia y Tabessan. Surge un visir envidioso que critica a Beremís. El elogio de los teóricos soñadores hecho por Beremís. El rey proclama la victoria de la teoría sobre el utilitarismo grosero.
En determinado momento el califa, que estaba de buen humor, se dirigió a Beremís y le dijo:
- ¿Qué pensáis, calculista, de mis lindas “adjamis”? [62] Ya habréis notado que son parecidísimas. Una de ellas se llama Iclimia [63] y la otra responde al tierno nombre de Tabessan. [64] Son gemelas y valen un tesoro. No encontré, hasta ahora, quien fuese capaz de distinguir, con seguridad, una de otra, cuando reaparecen después de danzar. Inclimia (¡mira bien!) es la que se encuentra ahora a la derecha; Tabessan, a la izquierda, junto a la columna nos dirige su mejor sonrisa.
- Confieso, oh sheik del Islam [65] –respondió Beremís- que vuestras bailarinas son, realmente, irresistibles. Loado sea Alah, el Único, que creó la Belleza para modelar con ella las seductoras formas femeninas. De la mujer hermosa ya dijo el poeta:
“Mujer no eres solo obra de Dios,Sin embargo, me parece relativamente fácil – añadió el calculista- distinguir a Iclinia de su hermana Tabessan, basta reparar en la hechura de los trajes de ambas.
los hombres te están creando eternamente
con la hermosura de sus corazones
y sus ansias han vestido de gloria tu juventud.”
“Por ti labra el poeta su tela de oro imaginaria;
el pintor regala a tu forma, día tras día, nueva inmortalidad.
Por adornarte, por vestirte, por hacerte más preciosa,
el mar da sus perlas, la tierra su oro, su flor los jardines del estío.”
“Mujer, eres mitad mujer y mitad sueño.”[66]
- ¡Cómo! –dijo el sultán-. Por los trajes no se podrá descubrir la menor diferencia, pues determiné que ambas usasen velos, blusas y mhazmas [67] rigurosamente iguales.
- Pido perdón, rey generoso – contradijo Beremís-, mas las costureras no acataron vuestra orden con el debido cuidado. La “mhazma” de Iclinia tiene en el borde, 312 franjas, mientras que la de Tabessan sólo posee 309 franjas. Esa diferencia de 3 franjas es suficiente para evitar la confusión entre las dos hermanas gemelas.
Al oír tales palabras, el califa batió palmas, haciendo parar el baile, y ordenó que un “haquim” [68] contase, una por una, todas las franjas que aparecían en las polleras de las bailarinas.
El resultado confirmó el cálculo de Beremís.
Iclinia tenía en el vestido 312 franjas y Tabessan 309.
- ¡Mac Alah! –exclamó el califa-. El sheik Iezid, a pesar de ser poeta, no exageró. Este calculista es realmente prodigioso. ¡Contó todas las franjas de las polleras mientras las bailarinas danzaban rápidamente sobre el tablado!
La envidia, cuando se apodera de un hombre, abre en su alma el camino a todos los sentimientos despreciables y torpes.
Había en la corte de Al-Motacen un visir llamado Nahun Ibn-Nahun, hombre malo y ruin. Viendo crecer ante el califa el prestigio de Beremís, como duna de arena formada por el simún, y aguijoneado por el despecho, ideó desprestigiar a mi talentoso amigo, colocándolo en situación falsa y ridícula. Con ese propósito se acercó al rey y le dijo:
- Acabo de observar, Emir de los Creyentes, que el calculista persa es hábil para contar los elementos o figuras de un conjunto. Contó las quinientas y tantas palabras escritas en las paredes del salón, citó dos números amigos, habló de la diferencia 64 (que es cubo y cuadrado), y terminó contando, una por una, las franjas de las polleras de las hermosas bailarinas djalcianas.
Quedaríamos mal servidos si nuestros matemáticos se dispusieran a observar solamente cosas tan pueriles y sin utilidad práctica alguna. Realmente. ¿Qué nos importa saber si hay en los versos que nos engrandecen, 220 ó 284 palabras, y si esos números son amigos o no? La preocupación de cuantos admiramos a un poeta, no es contar las letras de sus versos, ni calcular el número de ellas escritas en rojo o en negro. Tampoco nos interesa saber si en el vestido de esta bella y graciosa bailarina hay 309, 312 ó 1.000 franjas. Todo eso es ridículo y de muy escaso interés para los hombres de sentimiento que cultivan la Belleza y el Arte.
El ingenio humano, amparado por la ciencia, debe consagrarse a la resolución de los grandes problemas de la vida. Los sabios –inspirados por Alah, el Exaltado- no levantaron el deslumbrante edificio de la Matemática para que esa noble ciencia viniese a tener la aplicación que le encuentra el calculista persa. Me parece, pues, un crimen, reducir la ciencia de un Euclides, de un Arquímedes o de un maravilloso Omar Cayan (¡Alah lo tenga en su gloria!), a esa mísera situación de evaluadora numérica de cosas y seres. Nos interesa, pues, ver a ese calculista aplicar las teorías (que dice poseer) en la resolución de problemas de utilidad real, esto es, problemas que se relacionen con las necesidades de la vida corriente.
- Hay un pequeño engaño de vuestra parte, señor visir –replicó en seguida Beremís-, y yo tendría a gran honra esclarecer ese pequeño error si el generoso Califa, nuestro amo y señor, me concediera permiso para dirigirle más extensamente la palabra en esta audiencia.
- No deja de parecerme, hasta cierto punto, juiciosa –replicó el rey- la censura del visir Nahun Ibn-Nahun. Una aclaración sobre el caso es indispensable. Habla, pues. Tus palabras orientarán la opinión de los que aquí se hallan.
- Los doctores y “ulemas”, ¡Oh rey de los Árabes! –comenzó Beremís- no ignoran que la Matemática surgió con el despertar del alma humana; peor, no lo hizo con fines utilitarios. Fue el ansia de resolver el misterio del Universo, delante del cual los hombres son como granos de arena, que le dio el primer impulso. El verdadero desenvolvimiento resultó, ante todo, del esfuerzo en penetrar y comprender el Infinito. El progreso material de los hombres depende de las conquistas abstractas o científicas del presente, y es a los hombres de ciencia que trabajan sin ningún designio de aplicación de sus doctrinas, a los que la Humanidad será deudora en lo futuro [69]. Cuando el matemático efectúa sus cálculos o busca nuevas relaciones entre los números, no lo hace con fines utilitarios. Cultivar la ciencia por la utilidad práctica, inmediata, es desvirtuar el alma de la propia ciencia.
Aparece en la amonita (concha fósil perteneciente a un molusco cefalópodo) una curva considerada entre las figuras más notables – la “espiral logarítmica”.
Privilegio grande del matemático es esa ligazón íntima y misteriosa entre él y su aspiración, que, fuera de sí mismo, casi no interesa a nadie; análogamente decimos de las aplicaciones prácticas de la ciencia que apasionan a las multitudes, y frente a las cuales él permanece aparentemente ajeno. Que ese acuerdo entre las especulaciones matemáticas y la vida práctica se expliquen por medio de argumentos matemáticos o de teorías biológicas, no importa; lo cierto es que esa relación existe y que la Historia sólo ha logrado confirmarlo. En los estudios más áridos y abstractos el matemático trabaja convencido que su labor, hoy o mañana, será útil a sus semejantes. Esa certeza de la gran utilidad de su obra permite al matemático entregarse, sin reserva y sin remordimiento, a los placeres de la imaginación creadora, sin pensar más que en su propio ideal de belleza y verdad.¿La teoría estudiada hoy tendrá aplicaciones en lo futuro?
¿Quién podrá aclarar ese enigma ni su proyección, a través de los siglos? ¿Quién podrá, de la ecuación del presente, despejar la gran incógnita de los tiempos venideros? Sólo Alah sabe la verdad. Es muy posible que las investigaciones teóricas de hoy provean, dentro de mil o dos mil años, de preciosos recursos a la práctica. Es preciso, sin embargo, no olvidar que la Matemática, además del objetivo de resolver problemas, calcular áreas y medir volúmenes, tiene finalidades mucho más elevadas.
Por tener alto valor en el desenvolvimiento de la inteligencia y del raciocinio, es la Matemática uno de los caminos más seguros por donde puede llegar el hombre a sentir el poder del pensamiento, la magia del espíritu.
El estudio de la matemática contribuye, por sí sólo, a la formación de la personalidad; ante todo, ejercita singularmente la atención, y, de ese modo, desenvuelve, concomitantemente, la voluntad y la inteligencia; habitúa a reflexionar sobre una misma cosa que no ocupa los sentidos, a observarla en todos sus aspectos y en todas sus variantes, a compararla con otros objetos análogos, a descubrir tenues y ocultos vínculos, y a seguir, en todos sus pormenores, la extensa cadena de deducciones; de hábitos de paciencia, de precisión y de orden; inicia el razonamiento en los recursos de la Lógica; eleva y encanta por la contemplación de vastas teorías magníficamente ordenadas y resplandecientes de claridad.
La Matemática es, en fin, una de las verdades eternas y, como tal, eleva el espíritu –del mismo modo que lo hace la contemplación de los grandes espectáculos de la Naturaleza, a través de los cuales sentimos la presencia de Dios, Eterno y Omnipotente. Hay, pues, ilustre visir Nahun Ibn-Nahun, como ya dije, un pequeño error de vuestra parte. Cuento los versos de un poema, calculo la altura de una estrella, las franjas de una pollera, mido la extensión de un país, o la fuerza de un torrente; aplico, en fin, fórmulas algebraicas y principios geométricos, sin preocuparme por el beneficio inmediato que puedan producirme mis cálculos y estudios. Sin los sueños y las fantasías, la ciencia se empequeñecería; sería una ciencia muerta. ¡Uassalam!
Las palabras elocuentes de Beremís impresionaron profundamente a los nobles y “ulemas” que rodeaban el trono.
El rey se aproximó al calculista, y, estrechándole la mano, exclamó con gran autoridad:
- La teoría del hombre de ciencia soñador venció y vencerá siempre al utilitarismo grosero del ambicioso sin ideal filosófico.
Al oír tal sentencia, dictada por la justicia y por la razón, el envidioso Mahun Ibu-Hahun se inclinó, dirigió un “zalam” al rey, y sin decir palabra se retiró cabizbajo de la Sala de Audiencias.
Capítulo 15
En el cual Nuredin regresa a la Sala de Audiencias. La información que obtuvo de un “imman”. Como vivía el pobre calígrafo. El cuadrado lleno de números y el tablero de ajedrez. Beremís habla sobre los cuadrados mágicos. La consulta del “ulema”. El rey pide a Beremís que le cuente la leyenda del juego de ajedrez.
A relatar las medidas que tomara para dar cumplimiento a la orden del califa, habló así el noble musulmán:
- Salí de este palacio, acompañado por tres guardias, hacia la mezquita de Otman (Alah la ennoblezca cada vez más). Me informó un viejo “imman”, que vela por la conservación del templo, que el hombre que buscaba había, efectivamente, residido algunos meses en una casa próxima. Pocos días antes, sin embargo, salió para Basora, con una caravana de vendedores de tapices y velas. Supe también que el calígrafo (cuyo nombre el “imman” ignoraba) vivía sólo, y que raras veces dejaba la pequeña y modesta habitación en que moraba. Creí necesario examinar esa habitación, en procura de algún indicio que facilitase la pesquisa.
Cuadrado mágico de 9 casillas El aposento se hallaba abandonado desde el día en que el calígrafo lo dejara. Todo allí denotaba extraordinaria pobreza. Un lecho basto, colocado a un costado, era todo el mobiliario. Sobre un cajón tosco, de madera, un tablero de ajedrez y unas cuantas piezas de ese juego y, en las paredes, un cuadrado lleno de números. Encontrando extraño que un hombre tan pobre, que llevaba una vida llena de privaciones, cultivase el juego de ajedrez y adornase las paredes con figuras de expresiones matemáticas, resolví traer esos objetos conmigo, para que nuestros “ulemas” pudieran admirar las reliquias dejadas por el viejo calígrafo.
El sultán, lleno de curiosidad por el caso, ordenó a Beremís que examinase con la atención debida el tablero y la figura que parecía más apropiada para un discípulo de Al-Carismi [70], que para adorno del cuarto de un pobre.
Después de haber observado meticulosamente el tablero y el cuadro, dijo el “Hombre que calculaba”:
- Esa interesante figura numérica, encontrada en el cuarto del calígrafo, constituye lo que llamamos un “cuadrado mágico”.
Tomemos un cuadrado y dividámoslo en 9, 16, 25 ó más cuadrados iguales, que llamaremos casillas.
Cuadrado mágico chino, en el cual los números (por falta de guarismos), son representados por objetos. Parece pertenecer á 2800 años A. C. En cada una de esas casillas coloquemos un número entero. La figura obtenida será un cuadrado mágico cuando la suma de los números que figuran en una columna, en una fila, o en cualquiera de las diagonales, sea siempre la misma. Ese resultado invariable se llama constante del cuadrado, y el número de casillas de una fila, módulo del mismo.
Los números que ocupan las diferentes casillas del cuadrado mágico deben ser todos diferentes y tomados en su orden natural.
El origen de los cuadrados mágicos es oscuro. Se cree que la construcción de esas figuras constituía ya, en épocas remotas, un pasatiempo que absorbía la atención de gran número de curiosos.
Como los antiguos atribuían a ciertos números, propiedades cabalísticas, era muy natural que viesen virtudes mágicas en los arreglos especiales de esos números.
Los cuadrados mágicos eran conocidos por los matemáticos chinos que vivieron cuarenta y cinco siglos antes de Mahoma.
Es imposible, sin embargo, construir un cuadrado mágico con cuatro casillas.
En la India muchos reyes usaban los cuadrados mágicos como amuletos; un sabio de Yemen afirmaba que los cuadrados preservaban de ciertas enfermedades. Un cuadrado mágico de plata, colgado del cuello, evitaba, según la creencia de cierta tribu, el contagio de la peste.
Cuando un cuadrado mágico presenta cierta propiedad –como, por ejemplo, la de poder descomponerse en varios cuadrados mágicos –lleva el nombre de hipermágico.
Cuadrado mágico de 16 casillas, que los matemáticos llaman “diabólico”. La constante 34 de este cuadrado mágico no solamente se obtiene sumando los números de una misma columna, o de una misma fila, o de una diagonal, sino también sumando de otras maneras cuatro números del cuadro, por ejemplo, 4+5+11+14 = 34; 4+9+6+15 = 34; 1+11+16+6 = 34,… y así de 86 modos diferentes. Véanse nuestras Notas sobre cuadrados mágicos al final de este libro. Entre los cuadrados hipermágicos podemos citar los diabólicos. Así se denominan los cuadrados que continúan siendo mágicos aunque cambie una fila por una columna[71].
Las indicaciones hechas por Beremís acerca de los cuadrados mágicos fueron oídas con gran atención por el rey y por los nobles musulmanes.
Uno de los “ulemas”, después de dirigir elogiosas palabras al “eminente Beremís Samir, del país de Irán”, aseguró que deseaba hacer una consulta al sabio calculista. La consulta era la siguiente:
- ¿Habrá un método especial para las investigaciones matemáticas, o los grandes principios y las leyes admirables de esa ciencia serán descubiertas por casualidad?
La respuesta a esa delicada consulta la formuló Beremís en los siguientes términos:
- No existe, ni puede existir, método general para dirigir las investigaciones, pero es evidente que la casualidad casi no interviene. El descubrimiento es siempre producto de larga reflexión y de un esfuerzo consciente en una dirección ya determinada.
El hecho más interesante, entre los que observan entonces, es, tal vez, la aparición repentina de la solución largamente buscada, a veces cuando el investigador ya hace tiempo que abandonó el asunto. Todo permite creer que esa verdadera luz mental es el resultado de un trabajo subconsciente, que representaría un papel importante en el descubrimiento.
A continuación el brillante calculista tomó el tablero de ajedrez y dijo:
- Este viejo tablero, dividido en 64 casillas negras y blancas, se emplea, como sabéis, en un interesante juego que un hindú, llamado Lahur Sessa, inventó hace muchos siglos, para recreo de un rey de la India. El descubrimiento del juego de ajedrez se halla ligado a una leyenda que encierra cálculos y números.
- Debe ser interesante oírla –opinó el califa.
- Escucho y obedezco –respondió Beremís.
Y narró la historia siguiente:
Capítulo 16
Leyenda sobre el juego de ajedrez, contada al califa de Bagdad, Al-Motacen Billah, Emir de los Creyentes, por Beremís Samir, el “Hombre que calculaba”.
La guerra, con su cortejo inimitable de calamidades, amargó mucho la vida del rey Iadava, cambiando el ocio y el placer de que gozaba la realeza, en las más inquietantes tribulaciones. Fiel al deber que le imponía la Corona, de velar por la tranquilidad de sus súbditos, se vio el hombre bueno y generoso obligado a empuñar la espada para repeler, al frente de un pequeño ejército, un insólito y brutal ataque del aventurero Varangul, que se decía príncipe de Calian.
El choque violento de los dos rivales sembró de muertos los campos de Dacsina y tiñó de sangre las aguas sagradas del río Shandú. El rey Iadava tenía –según lo que revela la crítica de los historiadores- singular aptitud militar; sereno, elaboró un plan de batalla para impedir la invasión, y tan hábil y afortunado fue al ejecutarlo, que logró vencer y aniquilar por completo a los malintencionados perturbadores de la paz de su reino.
El triunfo sobre los fanáticos de Varangul le costó, desgraciadamente, grandes sacrificios; muchos jóvenes “quichatrias” [72] pagaron con la vida la seguridad de un trono para prestigio de una dinastía; y entre los muertos, con el pecho atravesado por certera flecha, quedó en el campo de batalla el príncipe Adjamir, hijo del rey Iadava, quien patrióticamente se sacrificó en el momento culminante de la lucha, para salvar la posición que dio a los suyos la victoria final.
Terminada la cruenta campaña y asegurados los nuevos límites de su frontera, regresó el rey a su suntuoso palacio de Andra, prohibiendo, sin embargo, las ruidosas manifestaciones con que los hindúes festejan sus victorias. Encerrado en sus habitaciones, solo salía de ellas para atender a los ministros y sabios brahmanes cuando algún grave problema nacional lo obligaba a decidir, como jefe de Estado, en interés y para la felicidad de sus súbditos.
Con el correr de los días, en lugar de pagarse los recuerdos de la penosa campaña, más se agravaban la angustia y la tristeza que, desde entonces, oprimían el corazón del rey. ¿De qué le podrían servir, en verdad, los ricos palacios, los elefantes de guerra, los tesoros inmensos, si ya no vivía a su lado aquel que fuera la razón de su existencia? ¿Qué valor podrían tener, a los ojos de un padre inconsolable, las riquezas materiales, que no borrarían nunca el recuerdo del hijo desaparecido?
Los pormenores de la batalla en que pereciera el príncipe Adjamir no abandonaban su pensamiento. El infeliz monarca pasaba largas horas trazando, sobre una gran caja de arena, las diversas maniobras realizadas por las tropas durante el asalto. Un surco indicaba la marcha de la infantería; otro, paralelo, a su lado, mostraba el avance de los elefantes de guerra; un poco más abajo, representada en pequeños círculos, dispuestos con simetría, se perfilada la temida caballería, comandada por un viejo “radj”[73], que se decía bajo la protección de Tchandra, la diosa de la Luna. Así, por medio de gráficos, esbozaba el rey la colocación de las tropas, estando las enemigas desventajosamente colocadas, gracias a su estrategia, en el campo en que se libró la batalla decisiva.
Una vez completo el cuadro de los combatientes, con todos los detalles que pudiera evocar, borraba el rey todo, y comenzaba otra vez, como si sintiese placer en revivir los momentos de angustia y ansiedad pasados.
A la hora temprana de la mañana, en que los brahmanes llegaban al palacio para la lectura de los Vedas [74], ya se veía al rey trazando en la arena los planos de una batalla que se reproducía indefinidamente.
¡Desgraciado monarca! –murmuraban los sacerdotes, apenados-. Procede como un “sudra”[75] a quien Dios privó del uso de la razón. ¡Sólo Dhanoutara [76], poderosa y clemente, podrá salvarlo!
Y los brahmanes elevaban oraciones, quemaban raíces aromáticas, implorando a la diosa clemente y poderosa, eterna patrona de los enfermos, que amparase al soberano de Taligana.
Un día, finalmente, fue informado el rey de que un joven brahmán –pobre y modesto- solicitaba una audiencia que venía pidiendo desde hacía algún tiempo. Como estuviese en ese momento en buena disposición de ánimo, ordenó el rey que llevaran al desconocido a su presencia.
Conducido a la gran sala del trono, fue interpelado el brahmán, como lo exigía la costumbre, por uno de los visires del rey.
- ¿Quién eres, de dónde vienes y que deseas de aquel que, por la voluntad de Vichnú[77], es rey y señor de Taligana?
- Mi nombre –respondió el, joven braman- es Lahur Sessa [78], y vengo de la aldea de Manir, que está a treinta días de marcha de esta bella ciudad. Al recinto en que vivía llegó la noticia de que nuestro bondadoso rey arrastraba los días, en medio de profunda tristeza, amargado por la ausencia del hijo que le robaba la guerra. Gran mal será pare el país, me dije, si nuestro querido soberano se encierra como un brahmán ciego dentro de su propio dolor.
Pensé, pues, en inventar un juego que pudiera distraerlo y abrir en su corazón las puertas a nuevas alegrías. Es ese insignificante obsequio que deseo, en este momento, ofrecer a nuestro rey Iadava.
Como todos los grandes principios citados en las páginas de la Historia, tenía el soberano hindú el grave defecto de ser excesivamente curioso. Cuando le informaron del objeto de que el joven bracmán era portador, no pudo contener el deseo de verlo y apreciarlo sin demora.
Lo que Sessa traía al rey Iadava consistía en un gran tablero cuadrado, dividido en sesenta y cuatro cuadraditos iguales; sobre ese tablero se colocaban dos colecciones de piezas, que se distinguían unas de otras por el color, blancas y negras, repitiendo simétricamente los motivos y subordinadas a reglas que permitían de varios modos su movimiento.
Sessa explicó con paciencia al rey, a los visires y cortesanos que rodeaban al monarca, en qué consistía el juego, enseñándoles las reglas esenciales:
- Cada uno de los jugadores dispone de ocho piezas pequeñitas, llamadas peones. Representan la infantería que avanza sobre el enemigo para dispersarlo. Secundando la acción de los peones vienen los elefantes de guerra[79], representados por piezas mayores y más poderosas; la caballería, indispensable en el combate, aparece, igualmente, en el juego, simbolizada por dos piezas que pueden saltar como dos corceles, sobre las otras; y para intensificar el ataque, se incluyen – representando a los guerreros nobles y de prestigio –los dos visires[80] del rey. Otra pieza, dotada de amplios movimientos, más eficiente y poderosa que las demás, representará el espíritu patriótico del pueblo y será llamada la reina. Completa la colección una pieza que aislada poco vale, pero que amparada por las otras se torna muy fuerte: es el rey.
El rey Iadava, interesado por las reglas del juego, no se cansaba de interrogar al inventor:
- ¿Y por qué la reina es más fuerte y poderosa que el mismo rey?
- Es más poderosa –argumentó Sessa- porque la reina representa, en el juego, el patriotismo del pueblo. El poder mayor con que cuenta el rey reside, precisamente, en la exaltación cívica de sus súbditos. ¿Cómo podría el rey resistir los ataques de sus adversarios, si no contase con el espíritu de abnegación y sacrificio de aquellos que lo rodean y velan por la integridad de la patria?
En pocas horas el monarca aprendió las reglas del juego, consiguiendo derrotar a sus visires en partidas que se desenvolvían impecablemente sobre el tablero.
Sessa, de vez en cuando, intervenía respetuoso, para aclarar una duda o sugerir un nuevo plan de ataque o de defensa.
En determinado momento el rey hizo notar, con gran sorpresa que la posición de las piezas, por las combinaciones resultantes de diversos lances, parecía reproducir exactamente la batalla de Dacsina.
- Observad –dijo el inteligente brahmán- que para conseguir la victoria es imprescindible el sacrificio de este visir.
E indicó precisamente la pieza que el rey Iadava, en el desarrollo del juego, pusiera gran empeño en defender y conservar.
El juicioso Sessa demostraba, de ese modo, que el sacrificio de un príncipe es a veces impuesto como una fatalidad, para que de él resulten la paz y la libertad de un pueblo.
Al oír tales palabras, exclamó el rey Iadava, sin ocultar su entusiasmo:
- No creí nunca, que el ingenio humano pudiera producir maravillas como este juego, tan interesante al par que instructivo. Moviendo esas simples piezas, aprendí que un rey nada vale sin el auxilio y la dedicación constante de sus súbditos, y que, a veces, el sacrificio de un simple peón vale más, para la victoria, que la pérdida de una poderosa pieza.
Y, dirigiéndose al joven brahmán le dijo:
- Quiero recompensarle, amigo mío, por este maravilloso obsequio, que de tanto me sirvió para aliviar viejas angustias. Pide, pues, lo que desees, para que yo pueda demostrar, una vez más, como soy de agradecido con aquellos que son dignos de una recompensa.
Las palabras con que el rey traducía su agradecimiento dejaron indiferente a Sessa. Su fisonomía serena no traducía la menor emoción ni la más insignificante muestra de alegría o sorpresa. Los visires miraban atónitos y asombrados su apatía ante un ofrecimiento tan magnánimo.
- Rey todopoderoso –recriminó el joven con suavidad y altivez. No deseo, por el presente que hoy os traje, otra recompensa que la satisfacción de haber proporcionado al señor de Taligana un pasatiempo agradable para aligerar el peso de las horas alargadas por agobiadora melancolía. Yo estoy, por lo tanto, sobradamente recompensado, y toda otra paga sería excesiva.
Sonrió, desdeñosamente, el bondadoso soberano al oír aquella respuesta, que reflejaba u desinterés tan raro entre los hindúes. Y, no creyendo en la sinceridad de las palabras de Sessa, insistió:
- Me causa asombro tanto desamor y desdén por las cosas materiales, joven. La modestia, cuando es excesiva, es como el viento que apaga la antorcha, dejando al viandante en las tinieblas de una noche interminable. Para que el hombre pueda vencer los múltiples obstáculos que le depara la vida, precisa tener el espíritu sujeto a una ambición que lo impulse hacia un ideal cualquiera. Exijo, por tanto, que escojas si demora, una recompensa digna de tu valioso regalo. ¿Quieres una bolsa llena de oro? ¿Deseas un arca llena de joyas? ¿Pensaste en poseer un palacio? ¿Aspiras a la administración de una provincia? Aguardo tu respuesta, ya que mi palabra está ligada a una promesa.
- No admitir vuestro ofrecimiento después de vuestras últimas palabras -respondió Sessa-, más que descortesía sería desobediencia al rey. Voy, pues, a aceptar por el juego que inventé, una recompensa que corresponda a vuestra generosidad; no deseo, sin embargo, ni oro, ni tierras, ni palacios. Deseo mi recompensa en granos de trigo.
- ¿Granos de trigo? –exclamó el rey, sin ocultar la sorpresa que le causara semejante propuesta-. ¿Cómo podré pagarle con tan insignificante moneda?
- Nada más simple –aclaró Sessa-. Dadme un grano de trigo por la primera casilla del tablero, dos por la segunda, cuatro por la tercera, ocho por la cuarta y así duplicando sucesivamente hasta la sexagésima cuarta y última casilla del tablero. Ruego a vos, rey generoso, que de acuerdo con vuestra magnífica oferta, ordenéis el pago en granos de trigo, y así como te indiqué.
No sólo el rey, sino los visires y venerables brahmanes, se rieron estrepitosamente al oír la extraña solicitud del joven. La falta de ambición que se traducía en aquel pedido era, en verdad, como para causar asombro aun al que menos apego tuviese a las cosas materiales de la vida. ¡El joven brahmán, que pudo obtener del rey un palacio o una provincia, se conformaba con granos de trigo!
- Insensato –exclamó el rey-. ¿Dónde aprendiste tan grande indiferencia por la fortuna? La recompensa que me pides es ridícula. Bien sabes que en un puñado de trigo hay un número enorme de granos. Debes darte cuenta de que con dos o tres medidas de trigo te pagaré holgadamente, conforme tu pedido, por las 64 casillas del tablero. Has elegido una recompensa que no alcanzaría ni para distraer algunos días el hambre del último “paria” [81] de mi reino. En fin, ya que mi palabra fue empeñada, ordenaré que el pago se haga inmediatamente conforme a tu deseo.
Mandó llamar el rey a los algebristas más hábiles de la Corte y les ordenó calculasen la porción de trigo que Sessa pretendía.
Los sabios matemáticos, al cabo de algunas horas de profundos estudios, volvieron al salón para hacer conocer al rey el resultado completo de sus cálculos.
Preguntóles el rey, interrumpiendo el juego:
- ¿Con cuántos granos de trigo podré cumplir, finalmente, con la promesa hecha al joven Sessa?
- Rey magnánimo –declaró el más sabio de los geómetras-: calculamos el número de granos de trigo que constituirá la recompensa elegida por Sessa, y obtuvimos un número cuya magnitud es inconcebible para la imaginación humana[82].
Hallamos en seguida, y con la mayor exactitud, a cuántas “ceiras” [83] correspondería ese número total de granos, y llegamos a la siguiente conclusión: la cantidad de trigo que debe entregarse a Lahur Sessa equivale a una montaña que teniendo por base la ciudad de Taligana, fuese 100 veces más alta que el Himalaya. La India entera, sembrados todos sus campos, y destruidas todas sus ciudades, no produciría en un siglo la cantidad de trigo que, por vuestra promesa, debe entregarse al joven Sessa.
¿Cómo describir aquí la sorpresa y el asombro que esas palabras causaron al rey Iadava y a sus dignos visires? El soberano hindú se veía, por primera vez, en la imposibilidad de cumplir una promesa.
Lahur Sessa –refiere la leyenda de la época-, como buen súbdito, no quiso dejar afligido a su soberano. Después de declarar públicamente que se desdecía del pedido que formulara, se dirigió respetuosamente al monarca y prosiguió:
- Maldita, ¡oh rey!, sobre la gran verdad que los brahmanes prudentes tantas veces repiten: los hombres más precavidos, eluden no solo la apariencia engañosa de los números sino también la falsa modestia de los ambiciosos. Infeliz de aquel que toma sobre sus hombros los compromisos de honor por una deuda cuya magnitud no puede valorar por sus propios medios. Más previsor es el que mucho pondera y poco promete.
Y después de ligera pausa, continuó:
- Aprendemos menos con las lecciones de los brahmanes que con la experiencia directa de la vida y de sus lecciones diarias, siempre desdeñadas. El hombre que más vive, más sujeto está a las inquietudes morales, aunque no quiera. Hállase ora triste, ora alegre; hoy vehemente, mañana indiferente; ya activo, ya indolente; la compostura, la corrección, alternará con la liviandad. Sólo el verdadero sabio, instruido en las reglas espirituales, se eleva por encima de esas vicisitudes, pasando por sobre todas esas alternativas.
Esas inesperadas y sabias palabras quedaron profundamente grabadas en el espíritu del rey. Olvidando la montaña de trigo que, si querer, prometiera al joven brahmán, lo nombró su primer ministro.
Y Lahur Sessa, distrayendo al rey con ingeniosas partidas de ajedrez y orientándolo con sabios y prudentes consejos, prestó los más señalados servicios a su pueblo y a su país, para mayor seguridad del trono y mayor gloria de su patria.
Encantado quedó el califa Al-Motacen cuando Beremís terminó la singular historia del juego de ajedrez. Llamó al jefe de sus escribas y ordenó que la leyenda de Sessa fuese escrita en hojas especiales de pergamino y conservada en hermoso cofre de plata.
En seguida, el generoso soberano ordenó se entregara al calculista un manto de honor y 100 sequíes de oro.
A todos causó gran alegría el acto de magnificencia del soberano de Bagdad. Los cortesanos que permanecían en la Sala de Audiencias eran todos amigos del visir Maluf y del poeta Iezid; era, pues, con simpatía, que oían las palabras del calculista persa, por quien se interesaban vivamente.
Beremís, después de agradecer al soberano los presentes con que acababa de ser distinguido, se retiró de la Sala de Audiencias. El califa iba a iniciar el estudio y a juzgar varios casos, oír a los “cadis” [84] y a dictar sus sabias sentencias.
Dejamos el palacio real al caer la noche y cuando comenzaba el mes de Cha-band[85].
Capítulo 17
En el cual el “Hombre que calculaba” recibe innumerables consultas. Creencias y supersticiones. Unidad y figura. El cuentista y el calculista. El caso de las 90 manzanas. La Ciencia y la Caridad.
Todos los días veíase obligado el calculista a atender decenas de consultas. Una vez era un cobrador de impuestos que necesitaba conocer el número de “ratls” impuestos en un “abás” y la relación entre esa unidad y el “cate”[86]; aparecía, en seguida, un “hequim” ansioso por oír a Beremís una explicación sobre la cura de ciertas fiebres por medio de siete nudos hechos en una cuerda; más de una vez el calculista fue llamado por los camelleros que querían saber cuántas veces debía un hombre saltar una hoguera para librarse del Demonio. Aparecían a veces, al caer de la noche, soldados turcos, de aviesa mirada, que deseaban aprender medios seguros para ganar en el juego de los dados. Tropecé, muchas veces, con mujeres –ocultas por espesos velos- que venían, tímidas, a consultar al matemático sobre los números que debían tatuarse en el antebrazo izquierdo para tener buena suerte, alegría y riqueza.
A todos atendía Beremís Samir con paciencia y bondad. Aclaraba las dudas a algunos, daba consejos a otros. Procuraba destruir las creencias y supersticiones de los mediocres e ignorantes, mostrándoles que ninguna relación puede existir., por la voluntad de Alah, entre los números y las alegrías o tristezas del corazón.
Y procedía así, guiado por elevado sentimiento de altruismo, sin perseguir lucro ni recompensas. Rechazaba sistemáticamente el dinero que le ofrecían, y cuando algún rico “sheik”, a quien enseñara, insistía en pagar la consulta, Beremís recibía la bolsa llena de denarios, agradecía la limosna y mandaba distribuirla íntegramente entre los pobres del barrio.
Cierta vez un mercader, llamado Aziz Neman, trayendo un papel lleno de números y cuentas, vino a quejarse de un socio, a quien llamaba “miserable ladrón”, “chacal inmundo” y otros epítetos no menos insultantes. Beremís procuró calmar el ánimo exaltado del comerciante, llamándolo al camino de la humildad.
- Cuídate –aconsejó- de los juicios hechos en un momento de arrebato, porque estos desfiguran muchas veces la verdad. Aquel que mira a través de un vidrio de color, ve todas las cosas del color de ese vidrio; si el vidrio es rojo, todo le parecerá rojizo; si es amarillo, todo se le presentará amarillento. El apasionamiento es para nosotros, lo que el color del vidrio para los ojos. Si alguien nos agrada, todo lo aplaudimos y disculpamos; si, por el contrario, nos molesta, todo lo condenamos o interpretamos de modo desfavorable.
En seguida examinó con paciencia las cuentas, y descubrió en ellas varios errores que desvirtuaban los resultados. Aziz se convenció de que había sido injusto con el socio, y quedó tan encantado con la manera inteligente y conciliadora de Beremís, que nos convidó aquella noche a efectuar un paseo por la ciudad.
Nos llevó nuestro cumplido compañero hasta el café Bazarique, situado en el extremo de la plaza de Otman.
Un famoso cuentista, en el medio de la sala llena de espeso humo, mantenía la atención de un numeroso grupo de oyentes.
Tuvimos la suerte de llegar en el preciso momento en el que el “sheik” El-Medah[87], habiendo terminado la acostumbrada oración inaugural, empezaba la narración. Era un hombre de más o menos cincuenta y seis años, moreno, de oscurísima barba y de ojos centellantes; usaba, como casi todos los cuentistas de Bagdad, un amplísimo paño blanco, ceñido en torno a su cabeza con una cuerda de pelo de camello, que le daba la majestad de un sacerdote antiguo. Hablaba en voz alta y enérgica erguido en medio del círculo de oyentes, acompañado por dos sumisos ejecutantes de laúd y tambor. Narraba, con entusiasmo, una historia de amor, intercalada con las vicisitudes de la vida de un sultán. Los oyentes, atentos, no perdían una sola palabra. El gesto del “sheik” era tan arrebatado, su voz tan expresiva y su rostro tan elocuente, que a veces daba la impresión de que vivía las aventuras que creaba su fantasía. Hablaba de un largo viaje; imitaba el paso del caballo cansado, y señalaba hacia grandes horizontes más allá del desierto. A veces fingía ser un beduino sediento procurando hallar a su alrededor una gota de agua; otras dejaba caer la cabeza y los brazos como un hombre postrado.
Árabes, armenios, egipcios, persas y nómades de Hedjaz, inmóviles, sin respirar, observaban atentos las expresiones del rostro del orador. En aquel momento, dejaban traslucir, con el alma en los ojos, toda la ingenuidad y frescura de sentimientos que ocultaban bajo una apariencia de salvaje dureza. El cuentista se movía para la derecha y para la izquierda, se cubría el rostro con las manos levantaba los brazos al cielo, y, a medida que aumentaba su entusiasmo y levantaba la voz, los músicos batían y tocaban con más fuerza. La narración entusiasmó a los beduinos; al terminar, los aplausos ensordecían.
El mercader Aziz Neman, que parecía muy popular en aquella barullenta reunión, se adelantó hacia el centro de la rueda y comunicó al “sheik”, en tono solemne y decidido:
- ¡Hállase presente el hermano de los árabes, el célebre Beremís Samir, el calculista persa, secretario del visir Maluf!
Centenares de ojos convergieron en Beremís, cuya presencia era un honor para los parroquianos del café.
El cuentista, después de dirigir un respetuoso “zalam” al “Hombre que calculaba”, dijo con bien timbrada voz:
- Mis amigos: he contado muchas historias de reyes, genios y magos. En homenaje al brillante calculista que acaba de entrar, voy a contar una historia que envuelve un problema cuya solución, hasta ahora, no fue descubierta.
- ¡Muy bien! ¡Muy bien! –exclamaron los oyentes.
El “sheik” evocó el nombre de Alah (¡con él en la oración y en la gloria!), y en seguida contó esta historia:
- Vivía una vez en Damasco un buen y trabajador aldeano que tenía tres hijas. Un día, conversando con un “cadí”, declaró el campesino que sus hijas estaban dotadas de gran inteligencia y de raro poder imaginativo.
El “cadí”, envidioso, irritose al oír elogiar al rústico el talento de las jóvenes, y dijo:
- Ya es la quinta vez que oigo de tu boca elogios exagerados que exaltan la sabiduría de tus hijas. Voy a probar si ellas son, como afirmas, tan ingeniosas y perspicaces.
Mandó el “cadí” llamar a las muchachas y les dijo:
- Aquí hay 90 manzanas que ustedes deberán vender en el mercado. Fátima, que es la mayor, llevará 50; Cunda llevará 30, y la pequeña Siha venderá las 10 restantes.
Si Fátima vende las manzanas a 7 por un denario, las otras deberán hacerlo por el mismo precio, esto es, a 7 por un denario; si Fátima fija como precio para la venta, tres denarios cada una, ese será el precio por el cual Cunda y Siha deberán vender las que llevan. El negocio debe hacerse de suerte que las tres saquen, con la venta de las respectivas manzanas, la misma cantidad.
- ¿Y no puedo deshacerme de algunas manzanas?, preguntó Fátima.
- De ningún modo –objetó, rápidamente, el impertinente “cadí”-. La condición, repito, es esa: Fátima debe vender 50, Cunda 30 y Siha sólo podrá vender las 10 que le tocan. Y por el precio que venda Fátima venderán las otras. Hagan las ventas de modo que al final los beneficios sean iguales.
Aquel problema, así planteado, resultaba absurdo y disparatado. ¿Cómo resolverlo? Las manzanas, según la condición impuesta por el “cadí”, debían ser vendidas por el mismo precio. En esas condiciones, era evidente que la venta de las 50 manzanas debía producir mayor beneficio que la venta de las 30 ó de las 10 restantes.
Como las jóvenes no atinaran con la forma de resolver el problema, fueron a consultar el caso con un imman[88] que vivía en la cercanía.
El imman, después de llenar varias hojas de números, fórmulas y ecuaciones, concluyó:
- Pequeñas: ese problema es de una simplicidad evidente. Vendan las 90 manzanas como el viejo cadí ordenó y llegarán sin error al resultado que él mismo determinó.
La indicación dada por el imman aclaraba el intrincado enigma de las 90 manzanas propuesto por el cadí.
Las jóvenes fueron al mercado y vendieron todas las manzanas: Fátima vendió las 50 que le correspondían, Cunda las 30 y Siha las 10 que llevara. El precio fue siempre el mismo para las tres, y el beneficio también. Aquí termina la historia. Toca ahora a nuestro calculista determinar cómo fue resuelto el problema.
No bien terminó el narrador de hablar, Beremís se encaminó al centro del círculo formado por los curiosos oyentes, y dijo así:
- No deja de ser interesante ese problema, presentado bajo forma de una historia. He oído muchas veces lo contrario; simples historias, disfrazadas de verdaderos problemas de Lógica o de Matemática. La solución para el enigma con que el malicioso cadí de Damasco quiso atormentar a las jóvenes campesinas, es la siguiente:
Fátima inició la venta fijando el precio de 7 manzanas en un denario. Vendió de ese modo, 49, y se quedó con 1, sacando en esa primera venta 7 denarios. Cunda, obligada a vender las 30 manzanas por el mismo precio, vendió 28 por 4 denarios, quedando con 2 de resto. Siha, que tenía una decena, vendió 7 por un denario y se quedó con 3 de resto.
Tenemos así, como primera faz del problema:
| Fátima | vendió | 49 | y se quedó con | 1 |
| Cunda | vendió | 28 | y se quedó con | 2 |
| Siha | vendió | 7 | y se quedó con | 3 |
A continuación decidió Fátima vender la manzana que le quedaba en 3 denarios. Cunda, según la condición impuesta por el cadí, vendió las 2 manzanas en 3 denarios cada una, obteniendo 6 denarios, y Siha vendió las 3 suyas del resto por 9 denarios, esto es, también a 3 denarios cada una:
El sheik El-Medah, encantado con la solución presentada por Beremís, exclamó, levantando los brazos:
- ¡Por la segunda sombra de Mahoma! Este joven calculista es realmente un genio. Es el primer “ulema” que descubre, sin hacer cuentas complicadas, la solución exacta y perfecta para el problema del cadí.
La multitud que llenaba el café de Otman, sugestionada por los elogios del sheik, vitoreó:
- ¡Bravo, bravo! ¡Alah ilumine al joven “ulema”!
Era muy posible que muchos hombres no hubieran entendido la explicación de Beremís. No obstante esa pequeña restricción, los aplausos eran generales y vibrantes.
Beremís, después de imponer silencio a la barullenta concurrencia, les dijo con vehemencia:
- Amigos míos: me veo obligado a confesar que no merezco el honroso título de “ulema”. Loco es aquel que se considera sabio cuando sólo mide la extensión de su ignorancia. ¿Qué puede valer la ciencia de los hombres delante de la ciencia de Dios?
Y antes de que ninguno de los presentes lo interrogase, narró lo siguiente:
- Hallábase cierta vez, en presencia de Masudí [89], el gran historiador musulmán, el alquimista Aidemir ben-Alí, quien se vanagloriaba de poseer todos los secretos científicos que le hacían dueño de la tierra. Ante tan descabellada presunción, Masudí observó:
- “Aidemir ben-Alí habla como habló otrora la hormiga que descubriera la gran montaña de azúcar.” Y, a fin de curar, de una vez para siempre, la vanidad sin límite del alquimista, el gran historiador así le contó: “Érase una vez una hormiguita que, vagando por el mundo, encontró una gran montaña de azúcar. Muy contenta con su descubrimiento, sacó de la montaña un grano y lo llevó a su hormiguero. –“¿Qué es eso?”, preguntaron sus compañeras. –“Esto es una montaña de azúcar”, replicó orgullosa. “La encontré en mi camino y resolví traerla para aquí.” –Masudí, con maliciosa ironía, concluyó así: -El sabio orgulloso es como la hormiga. ¡Trae una pequeña migaja, y casi cree llevar el propio Himalaya! La ciencia es una gran montaña de azúcar; de esa montaña sólo conseguimos retirar insignificantes trocitos.”
Un barquero de hinchadas mejillas, que se hallaba en la rueda, preguntó a Beremís:
- ¿Cuál es la ciencia de Dios?
- ¡La ciencia de Dios es la Caridad!
En ese momento me acordé de la admirable poesía que oyera a Telassim, en los jardines del “sheik” Iezid, cuando los pájaros fueron puestos en libertad:
Si yo hablase las lenguas de los hombres
y de los ángeles
y no tuviese caridad,
sería como el metal que suena,
o como la campana que tañe,
¡Nada sería!...
¡Nada sería!...
Hacia la media noche, cuando dejamos el café Bazarique, varios hombres, para testimoniarnos la consideración que nos dispensaban, vinieron a ofrecernos sus pesadas linternas, pues la noche era oscura y las calles eran tortuosas y estaban desiertas.
Capítulo 18
En el cual volvemos al palacio del sheik Iezid. Una reunión de poetas y letrados. El homenaje al Maharajá de Laore. La Matemática en la India. La perla de Lilavati. Los problemas de Aritmética de los hindúes. El precio de la esclava de 20 años.
- Todavía es muy temprano para la clase (advirtió tranquilo, Beremís). Dudo que mi paciente alumna haya sido prevenida.
El egipcio explicó que el “sheik”, antes de la clase de Matemática, deseaba presentar al calculista a su grupo de amigos. Convenía, pues, llegar más temprano al palacio del poeta.
Esta vez, por precaución, fuimos acompañados por tres esclavos negros, decididos y fuertes, pues era muy posible que el terrible y celoso Tara-Tir intentase, en el camino, asaltarnos y matar al calculista, en el cual, parece, preveía a un poderoso rival.
Una hora después, sin que nada anormal ocurriera, llegamos a la magnífica residencia del “sheik” Iezid. El esclavo egipcio nos condujo, a través de interminable galería, hasta un hermoso salón azul adornado con frisos dorados. Alí se encontraba el padre de Telassim, rodeado de varios letrados y poetas.
- ¡Zalam aleikum!
- ¡Masa al-quair, sheik!
- ¡Venta ezzaiac!
Cambiados esos atentos saludos, el dueño de casa nos dirigió unas palabras amistosas convidándonos a tomar parte en aquella reunión.
Nos sentamos, sobre blandos cojines de seda. Una esclava morena, de ojos negros y vivaces, nos trajo frutas, dulces secos y agua perfumada con rosas.
Observé entonces que uno de los invitados que parecía extranjero, ostentaba en sus trajes un lujo excepcional.
Vestía una túnica de satín blanco de Génova, sostenida con un cinturón azul adornado con brillantes, y del cual colgaba un lindo puñal con el cabo de lapislázuli y zafiros. El turbante, de seda color rosa, adornado con hilos negros, tenía diseminadas piedras preciosas, y sus manos, trigueñas y finas, se veían realzadas por el brillo de los anillos que cubrían los dedos.
- Ilustre geómetra –dijo el sheik Iezid, dirigiéndose al calculista-: noto bien que estáis sorprendido con la reunión que promoví hoy en esta humilde tienda. Debo, por tanto, informaros que esta reunión no tiene otra finalidad que la de tributar homenaje a nuestro ilustre huésped, el príncipe Cluzir-el-din Meubareo-Scha señor de Loare y Delhi.
Beremís con una leve inclinación de busto hizo un “zalam” al gran maharajá de Laore, que era el joven del cinto de brillantes.
Ya sabíamos, por las conversaciones habituales con que nos entretenían los forasteros de la posada, que el príncipe había dejado sus ricos dominios de la India para cumplir con uno de los deberes de todo buen musulmán: hacer la peregrinación a la Meca, la perla del Islam. Quedaría, por lo tanto, pocos días en Bagdad, para continuar luego, con sus numerosos siervos y ayudantes, hacia la Ciudad Santa.
- Deseamos, calculista –prosiguió Iezid- tu ayuda para que podamos aclarar una deuda sugerida por el príncipe Cluzir Schá. ¿Cuál fue la contribución con que la ciencia de los hindúes enriqueció a la Matemática? ¿Cuáles los principales geómetras que más se destacaron en la India por sus estudios e investigaciones?
- Generoso sheik –respondió Beremís-. La tarea que acabáis de encomendarme es de las que exigen erudición y serenidad. Erudición para conocer, con todos los detalles, los datos recopilados por la Historia de las Ciencias y serenidad para analizarlos y juzgarlos con elevación y discernimiento. Vuestros menores deseos, oh sheik, son, sin embargo, órdenes para mí. Expondré en esta brillante reunión, como humilde homenaje al príncipe Cluzir Schá (a quien recién he tenido el honor de conocer), las pocas nociones que aprendí en los libros sobre el desenvolvimiento de la Matemática en el país de Ganges.
Y así comenzó el “Hombre que calculaba”:
- Nueve o diez siglos antes de Mahoma, vivió en la India un bracmán ilustre que se llamaba Apastamba. Con el objeto de informar a los sacerdotes sobre los procedimientos para construir altares y orientar los templos, escribió ese sabio una obra intitulada Suba-Sultra, que contiene numerosas enseñanzas matemáticas. Es poco probable que esa obra haya recibido la influencia de los Pitagóricos [91], pues la Geometría del sacerdote hindú no sigue el método de los investigadores griegos. En las páginas de Suba-Sultra se encuentran varios teoremas de Matemática y pequeñas reglas sobre construcciones de figuras. Para transformar convenientemente un altar, el prudente Apastamba construye un triángulo rectángulo cuyos lados miden, respectivamente, 39, 36 y 15. Aplica en la solución de este interesante problema el principio famoso atribuido al geómetra Pitágoras:
“El cuadrado construido sobre la hipotenusa es equivalente a la suma de los cuadrados construidos sobre los catetos.”
El teorema de Pitágoras, tan citado en Matemática, puede demostrarse de muchísimas maneras. Siendo A el área del cuadrado construido sobre la hipotenusa, B y C las de los cuadrados construidos sobre los catetos, tenemos la siguiente relación: A = B + C. La figura que traduce el teorema de Pitágoras es clásica en Matemática.
Esa proposición, señores, expresa una gran verdad. Ley eterna dictada por Dios y que la Ciencia reveló a los hombres. Antes que existiese Marte, o la Tierra o el Sol, y mucho después que dejaren de existir aquí como allá, en los mundos visibles como invisibles, -“el cuadrado construido sobre la hipotenusa fue y será siempre equivalente a la suma de los cuadrados construidos sobre los catetos.” Todas nuestras teorías de la vida, todas las pueriles especulaciones nuestras sobre la muerte, todas las discusiones sobre los problemas del destino –todo eso es polvareda que apenas se ve en un rayo de sol, comparado con la doble eternidad, pasada y futura, de una verdad como aquella.
Pues bien; el teorema de Pitágoras es presentado por el hindú Apastamba bajo una forma muy interesante:
“La diagonal de un rectángulo produce, por si sola, lo que los lados del rectángulo producen en conjunto.”
Es posible sacar en conclusión, pues, que los hindúes, sin el auxilio de los griegos, ya conocían los triángulos rectángulos, cuyos lados están expresados por números enteros. En el primer capítulo de Suba-Sultra hay referencias al triángulo rectángulo notable, cuyos lados miden, respectivamente, 3, 4 y 5. El ilustre Apastamba menciona otros triángulos pitagóricos:
12, 16,20;
5, 12,13;
8, 15,17
y llega, por medio de fracciones simples a expresar el valor aproximado de la raíz cuadrada de 2. [92]
Figura que podría servir para demostrar gráficamente el teorema de Pitágoras. Los lados del triángulo miden respectivamente 5, 4 y 3. La relación pitagórica se verifica con la igualdad: 25 = 16 + 9
El valor así obtenido, Apastamba lo aplica en la construcción de un cuadrado por medio de un ingenioso artificio.Los sacerdotes aprendían así, por la lectura de las páginas de Suba-Sultra, a transformar un rectángulo en un cuadro equivalente, cosa que, a veces, precisaban al tener que alterar la forma de un altar, sin modificar el área.
Surgieron después de Suba-Sultra varias obras de indiscutible valor en la Historia de la Matemática. Por ejemplo, Suria-Sidanta, que contiene una tabla de senos [93] utilizada por los astrónomos. La palabra seno, en idioma hindú, significa declive.
Triángulo rectángulo ya conocido y citado por los antiguos matemáticos hindúes. Conviene observar que el cuadrado (25) del lado mayor es igual a la suma de los cuadrados (9 + 16) de los otros dos lados
Suria-Sidanta es el primer tratado que expone las reglas de la numeración decimal cada guarismo tiene un valor negativo y emplea el cero para indicar la ausencia de unidades de cierto orden.
No menos notable, para la ciencia de los brahmanes, es el tratado de Aria-Bata, que se divide en cuatro partes: “Armonías Celestes”, “El Tiempo y su Medida”, “Las Esferas” y “ Elementos de Cálculo”. Varios son los errores que se observan en las páginas de Aria-Bata. Ese geómetra afirma que el volumen de una pirámide se obtiene “multiplicado la mitad de la base por la altura” [94] e indica como fórmulas para el cálculo de áreas de cuadriláteros, algunas que sólo son aplicables a casos particulares. Para determinar el largo de la circunferencia da Aria-Bata la siguiente regla: “Sumar 4 á 100, multiplicar por 8, sumar 62.000”; se obtiene así la longitud de la circunferencia para un círculo de dos miriámetros de diámetro. [95]
Los Pitagóricos fueron atacados de todos modos por sus adversarios. Con estas caricaturas pretendían ridiculizar a los discípulos del célebre filósofo griego.
Una de las más curiosas e importantes obras de la literatura científica de la India es Bijaganita.Ese nombre singular está formado por dos palabras, bija yganita, que significan, respectivamente, semilla y cuenta. La traducción perfecta del título de la obra hindú sería: “El arte de contar semillas”.
Lilavati, según una curiosa leyenda, no se casó por causa de una perla desprendida de su vestido de novia, y “que hizo detener el tiempo”. Báskara, el geómetra hindú, para consolar a su hija le dijo: “- Escribiré un libro que perpetuará tu nombre. Vivirás en el recuerdo de los hombres más de lo que hubieran vivido los hijos que pudieron haber nacido en tu malogrado matrimonio.” La obra de Báskara se hizo célebre y el nombre de Lilavati surge inmortal en la Historia de la Matemática.
El autor de ese trabajo extraordinario es el famoso matemático Báskara Acharia, que nació en Bidon, en la provincia de Decan, en el año 492 de la Hégira.[96] A más de Bijaganita escribió Báskara el célebre Lilavati, tratado de Álgebra y Geometría, y en los últimos años de su existencia hizo un pequeño libro de Astronomía, de relativa importancia, intitulado Suomani.
Es curioso el artificio que Báskara, matemático hindú, en su libro Lilavati, empleara para la determinación del área del círculo. Trazado un diámetro, cada uno de los semicírculos era dividido en un mismo número de sectores iguales. Los sectores 1, 2, 3, 4, 5, 6, 7, 8 y 9 que formaban uno de los semicírculos eran colocados como indica la figura, con las bases (que se suponen rectificadas) apoyadas sobre una recta AB. Los sectores a, b, c, d, e, f, g, h, i, que formaban el otro semicírculo eran colocados entre los primeros en oposición (como indica la figura) de modo de completar el paralelogramo ABCD. El área del círculo será igual al producto de la semicircunferencia por la altura (?) del círculo. La base AB de ese paralelogramo es la semicircunferencia rectificada (?).
El origen de Lilavati es muy interesante. Voy a relatarlo. Báskara tenía una hija llamada Lilavati. Cuando esta nació, él consultó a las estrellas y verificó, por la disposición de los astros, que su hija estaba condenada a quedar soltera toda la vida, no siendo requerida por los jóvenes nobles. Báskara no se conformó con esa determinación del Destino y recurrió a los astrólogos más famosos de la época. ¿Cómo hacer para que la graciosa Lilavati pudiese encontrar esposo, y ser feliz en el casamiento? Uno de los astrólogos consultados por Báskara, le aconsejó casar a Lilavati con el primer pretendiente que apareciera, pero dijo que la hora propicia para la ceremonia del enlace sería marcada, en cierto día, por el cilindro del Tiempo.Los hindúes medían, calculaban y determinaban las horas del día con ayuda de un cilindro colocado en un recipiente lleno de agua. Ese cilindro, abierto apenas en su parte superior, tenía un pequeño orificio en el centro de la base. La cantidad de agua que entraba por el orificio llenaba lentamente el cilindro que se iba hundiendo hasta desaparecer completamente bajo el agua a una hora previamente determinada.
Con agradable sorpresa para su padre, Lilavati fue pedida en matrimonio por un joven rico y de buena familia. Fijado el día y señalada la hora, se reunieron los amigos para asistir a la ceremonia.
Esta es Lilavati, la heroína de la célebre leyenda de “La perla y el tiempo”, que es llamada en el libro de Báskara “la linda pequeña de los ojos fascinantes”.
Báskara colocó el cilindro de las horas y aguardó que el agua llegase al nivel marcado. La novia, llevada por irresistible y verdaderamente femenina curiosidad, quiso observar la subida del agua en el cilindro. Al aproximarse para acompañar la determinación del Tiempo, una de las perlas de sus vestidos se desprendió y cayó dentro del vaso.Por una fatalidad, la perla, llevada por el agua, obstruyó el pequeño orificio del cilindro, impidiendo que pudiese entrar el agua. El novio y los convidados esperaron largo rato con paciencia. Pasó la hora fijada sin que el cilindro marcara el tiempo, como previera el sabio astrólogo. El novio y los convidados se retiraron para que fuese fijada otra fecha, después de consultar los astros.
El joven brahmán desapareció algunas semanas después, y la hija de Báskara quedó para siempre soltera.
Reconoció el inteligente geómetra que era inútil luchar contra el Destino y dijo a su hija:
Escribiré un libro que perpetuará tu nombre. Vivirás en el pensamiento de los hombres más de lo que hubieran vivido los hijos que pudieron haber nacido de tu malogrado matrimonio.
La obra de Báskara se hizo célebre y el nombre de su hija surge inmortal en la Historia de la Matemática.
En lo que se refiere a la Aritmética, Lilavati hace de las operaciones aritméticas sobre números enteros; estudia minuciosamente las cuatro operaciones, el problema de elevación al cuadrado y al cubo; enseña la extracción de la raíz cuadrada, y llega hasta el estudio de la raíz cúbica de un número cualquiera. Aborda después las operaciones con números fraccionarios, aplicando la hoy tan conocida regla de reducción a común denominador. Al final de esa parte, refiriéndose a la reducción de un número por cero[97], Báskara dice: “Ni la adición ni la sustracción, por grandes que sean, hacen disminuir o aumentar la cantidad llamada cociente por cero.”
Lilavati presenta, en seguida, reglas variadas de cálculo, algunas de carácter general, como la de inversión, que consiste, procediendo en orden inverso, en hallar un número que, sometido a una sucesión de operaciones, reproduzca un número dado, y la regla de falsa posición, que los Egipcios y los Griegos ya conocían y empleaban.
Interesantes por la forma, delicada algunas veces, rica y exuberante otras, como son presentados algunos problemas, revelan, por sus enunciados, la íntima satisfacción de quien los propuso, así como la inclinación de su espíritu a lo hermoso y al bien.
Es este un ejemplo característico:
“Amable y querida Lilavati, de dulces ojos como los de la delicada y tierna gacela, dime cuáles son los números que resultan de la multiplicación de 135 por 12.”
Más adelante Báskara enseña a resolver la siguiente y delicada cuestión:
“Linda pequeña de ojos fascinantes, tú, que conoces el verdadero método de la inversión, dime cual es el número que multiplicado por 3, aumentado en las tres cuartas partes del producto, dividido por 7, disminuido en un tercio del cociente, multiplicado por sí mismo, disminuido en 52, después de la extracción de la raíz cuadrada, adicionado en 8 y dividido por 10, sea 2.”[98]
No es menos interesante el problema formulado sobre un enjambre de abejas:
“La quinta parte de un enjambre de abejas se posa sobre una flor de kadamba, la tercera parte en una flor de silinda, el triple de la diferencia entre estos dos números vuela sobre una flor de krutja, y una abeja vuela indecisa de una flor de pandanus a un jazmín.”
Otros problemas tratan sobre el interés del dinero, sobre el precio de las esclavas, cuyo valor máximo, a los 16 años, correspondía al de 8 bueyes con dos años de trabajo, sobre el costo de los géneros, de los salarios, de los trasportes, etc.
El problema que relataré es uno de los incluidos en Lilavati y que pocos matemáticos sabrán resolver:
“Una pequeña de seis años es vendida por 32 niscas. ¿Cuál es el precio, en niscas, de una jovencita de 20 años?”
Es muy interesante también, la regla que Lilivati presenta para la determinación del área del círculo.
Capítulo 19
En el cual el príncipe Cluzir elogia al “Hombre que calculaba”. El problema de los tres marineros. La generosidad del Maharajá de Laore. Beremís recuerda los versos de un poeta. La ciencia y el mar.
- He quedado encantado –añadió- al oír la leyenda de la infeliz Lilavati, que perdió el novio por causa de una perla de su vestido. Los problemas de Báskara, citados por el elocuente calculista, son, realmente interesantes, y presentan, en sus enunciados, ese “espíritu poético”, que es tan difícil de hallar en las obras de Matemática. Siento, sin embargo, que el ilustre matemático no haya citado el famoso problema de los tres marineros, que aparece en el libro intitulado “Faiouentchoutin”, y que hasta ahora no tiene solución.
- Príncipe magnánimo –respondió Beremís-. Entre los problemas de Báskara por mi citados no figuró el de los tres marineros, por la simple razón que no lo conozco sino vagamente, por un relato incierto y dudoso, ignorando su enunciado exacto.
- Yo lo conozco perfectamente –dijo el príncipe-. Y tendría verdadero placer en recordar ahora esa cuestión, que tiene atribulados a tantos algebristas.
Y el príncipe Cluzir-Schá contó lo siguiente:
- Un navío que volvía de Serendibe [99], trayendo gran cantidad de especias, fue alcanzado por violento temporal. La embarcación habría sido destruida por las olas, si no fuera por el valor y el esfuerzo de tres marineros que, en medio de la tormenta, manejaban las velas con extremada pericia. El capitán, queriendo recompensar a los denodados marineros, les dio cierto número de “catils”. Los “catils” [100] eran más de doscientos y menos de trescientos. Las monedas fueron colocadas en una caja para que al día siguiente, al desembarcar, el almojarife [101] las repartiese entre los tres valientes. Sucedió, sin embargo, que durante la noche, uno de los tres marineros se despertó y pensó: “Sería mejor que retirase mi parte. Así no tendré oportunidad de discutir con mis amigos.” Y, sin decir nada a los compañeros, fue, en puntas de pié, hasta donde se hallaba guardado el dinero, lo dividió en tres partes iguales y notó que la división no era exacta, ya que sobraba un “catil”. –“Por causa de esta mísera monedita, es probable que mañana haya riña y discusión. Será mejor sacarla.” Y el marinero la tiró al mar, retirándose cauteloso. Llevaba su parte y dejaba las que correspondían a sus compañeros en el mismo lugar. Horas después el segundo marinero tuvo la misma idea. Fue al arca en que se depositara el premio colectivo y lo dividió en tres partes iguales. Sobraba una moneda. El marinero optó por tirarla al mar, para evitar posibles discusiones. Y salió de allí llevando la parte que creía le correspondía. El tercer marinero, ignorando, por completo, que sus compañeros se le habían anticipado, tuvo el mismo pensamiento. Levantóse de madrugada y fue a la caja de los “catils”. Dividió las monedas que en ella encontró, y la división tampoco resultó exacta; sobró un “catil”. No queriendo complicar el reparto, el marinero la tiró al mar y regresó satisfecho a su litera. Al día siguiente, al desembarcar, el almojarife encontró un puñado de “catils” en la caja. Sabiendo que esas monedas pertenecían a los marineros, las dividió en tres porciones, que repartió entre sus dueños. Tampoco fue exacta la división. Sobraba una moneda, que el almojarife se guardó como retribución a su trabajo y habilidad. Es claro que ninguno de los marineros reclamó, pues cada uno estaba convencido de haber retirado su parte. Ahora bien: ¿cuántas eran las monedas? ¿Cuánto recibió cada marinero?
Monedas en la caja | Dividas entre: | Da: | Resta: | Monedas restantes | |
241 | 3 | 80 | 1 | 160 | División hecha por el 1.er marinero. Dividiendo 241 por 3 da 80 y sobra 1 |
160 | 3 | 53 | 1 | 106 | División hecha por el 2º marinero. Dividiendo 160 por 3 da 53 y sobra 1 |
106 | 3 | 35 | 1 | 70 | División hecha por el 3.er marinero. Dividiendo 106 por 3 da 35 y sobra 1 |
70 | 3 | 23 | 1 | Última división: dividiendo 70 por 3 da 23 y sobra 1 |
El “Hombre que calculaba”, notando que la historia narrada por él, el príncipe despertara gran interés entre los nobles presentes, creyó necesario dar la solución completa del problema, y así lo hizo:
- Las monedas eran, al principio, 241. El primer marinero las dividió en tres partes; tiró un “catil” al mar y se llevó un tercio de 240, o sea, 80 monedas, dejando 160. El segundo marinero halló, por lo tanto, 160 monedas; tiró una al mar y dividió las restantes (159) en tres partes. Tomó la tercera parte, o sea, 53, y dejó el resto, 106. El tercer marinero encontró en la caja 106 monedas, dividió ese resto en tres partes iguales, tirando al mar la moneda que sobraba. Retiró la tercera parte de 105, o sea, 35 monedas, dejando el resto, o sea 70.
El almojarife encontró 70 monedas, las dividió en tres partes iguales, tocando 23 monedas más a cada marinero. El reparto fue hecho, por lo tanto, de la manera siguiente:
Marinero Nº 1 | 80+23 | = | 103 |
Marinero Nº 2 | 53+23 | = | 76 |
Marinero Nº 3 | 35+23 | = | 58 |
Almojarife | = | 1 | |
Tiradas al mar | = | 3 | |
Total | = | 241 |
Al llegar al final de la solución [102], y habiendo dejado de hablar Beremís, el príncipe, para demostrar su admiración por el ingenio del calculista, le ofreció como recompensa una pequeña medallita recubierta de rubíes.
- Esta joya –explicó sonriente el soberano hindú- fue grabada por un artista genial. En una de las caras aparece mi nombre entrelazado con una flor de loto; y la otra contiene algunos versos sobre el mar, escritos en lenguaje simbólico.
Beremís se mostró emocionado con el presente del príncipe y, tomando la medalla entre sus manos, la examinó con vivo interés.
- Es raro –dijo al fin-, peor el artista que imaginó esta delicada obra de arte se equivocó, sin querer. No encuentro aquí, ninguna poesía sobre el mar. Solo leo pensamientos sobre el Saber y la Ciencia:
“El que procura instruirse es más amado por Dios que aquel que combate en una guerra santa.”
“Aquel que educa y proporciona instrucción a los ignorantes, es como un vivo entre los muertos.”
“Si pasara un día sin que aprendiera alguna cosa que me aproximase a Dios, que la aurora de ese día no sea bendecida.”
“Es un sacrilegio prohibir la Ciencia. Pedir a la Ciencia es ofrecer actos de adoración a Dios; enseñarla, es hacer caridad. La ciencia es la vida del Islam, la columna de la Fe.”
- Amigo mío –dijo el poeta Iezid-. Conozco todos esos pensamientos. Fueron dictados por Mahoma (¡con Él en la oración y en la gloria!) y se enseñan hoy en todas las escuelas.
El sheik sonrió y concluyó:
- A mi modo de ver, el artista que grabó esa medalla no engañó al príncipe. La ciencia, según todos dicen, es un mar inmenso y profundo. Por consiguiente, esos pensamientos, desde el punto de vista simbólico, son “versos sobre el mar”.
Capítulo 20
En el cual Beremís da la segunda clase de Matemática. Número y sentido del mismo. Las diferentes definiciones de número. Los guarismos. Los sistemas de numeración. Numeración decimal. El cero. Oímos nuevamente la voz de la alumna invisible. El gramático Doreid, cita un poeta.
Después de saludar al príncipe y a los sheiks que conversaban en el salón, Beremís, acompañado de una esclava se encaminó hacia el aposento preparado para la lección.
Me levanté yo también, y acompañé al calculista, ya que tenía autorización para asistir a las lecciones dadas a la joven Telassim.
Uno de los presentes, el gramático Doreid, amigo del dueño de la casa, también deseó oír la lección y, dejando la compañía del príncipe Cluzir Schá, nos siguió. Doreid era un hombre de mediana edad, muy alegre, de rostro anguloso y expresivo.
Atravesamos una suntuosa galería tapizada con gobelinos y, guiados por una esclava circasiana de esplendorosa belleza, llegamos, al fin, a la sala de Matemática. El primitivo cortinado rojo que ocultaba a Telassim había sido sustituido por otro azul que tenía en el centro un gran heptágono estrellado.
Resulta interesante observar las diversas formas dadas a las cifras usuales al correr de los siglos. En el cuadro de arriba podemos observar, a partir de la primera columna de la izquierda, los guarismos 1, 2, 3, 4 y 5. En la primera fila, las cifras son apenas iniciales de las palabras del sánscrito (antiguo idioma de los bracmanes). En la tercera fila aparecen las primitivas cifras hindúes. En las dos últimas filas se ven las usadas hasta principios del siglo XVI.
El gramático Doreid y yo nos sentamos a un costado de la sala, cerca de la ventana que abría al jardín, Beremís se acomodó como la primera vez, bien en el centro, sobre un amplio cojín de seda.
Este cuadro muestra la evolución de las formas atribuidas a los guarismos 6, 7, 8 y 9 durante treinta siglos. Es interesante hacer notar que el número 8 (ocho) es el único que se mantuvo más o menos constante durante ese largo período de tiempo. El 9 (nueve) tomó la forma que presenta actualmente a partir del siglo XV.
A su lado, sobre una mesita de ébano, había un ejemplar del Corán. La esclava circasiana, de confianza del sheik Iezid, y otra persa, de ojos dulces y sonrientes, se apostaron junto a la puerta. El egipcio, encargado de la guardia personal de Telassim, se recostó indolente contra una columna.Después de la oración, así habló Beremís:
- No sabemos, señora, cuando la atención del hombre fue despertada por la idea de número. Las investigaciones hechas por los filósofos se remontan a los tiempos que solo se perciben a través de las nebulosas del pasado.
En 1579 el matemático italiano Bombelli incluyó en su Álgebra un conjunto completo de notaciones con las que pretendió simplificar el cálculo y facilitar las operaciones algebraicas. La raíz cuadrada era representada por las letras R, q, colocadas antes del radicando, y la raíz cúbica por un símbolo análogo R, c. nos nuestra la figura adjunta, en la primera línea una expresión algebraica escrita por Bombelli y, debajo, la misma expresión escrita con símbolos modernos. Dejó de ser incluida la letra p (signo de adición) antes de la segunda R.
Los que estudian la evolución del número demuestran que, entre los hombres primitivos, ya estaba la inteligencia humana dotada de lo que llamaremos el “sentido de número”. Esta facultad permite reconocer, de manera puramente visual, si un conjunto de objetos fue aumentado o disminuido, o sea, si sufrió modificación numérica.No se debe confundir el sentido de número con la facultad de contar. Solo la inteligencia humana es capaz de poseer el grado de abstracción que permite contar, mientras que el sentido de número es observado entre muchos animales.
Algunos pájaros, por ejemplo, sin contar los huevos que dejan en el nido, pueden distinguir dos de tres. Ciertas avispas llegan a distinguir cinco de diez.
Los salvajes de una tribu del norte de África conocían todos los colores del arco-iris y designaban cada uno por su nombre. Pues bien, esa tribu no conocía la palabra correspondiente al color. Así también, muchos idiomas primitivos presentan palabras para designar, uno, dos, tres,… etc., y no encontramos, en esos idiomas, un vocablo especial para designar el número, de un modo general.
Yo tuve ocasión de verificar, al hacer una excursión a país de Hadjad, que el número cuatro, entre los habitantes de Barnhein [103], era designado por dos nombres distintos: “Cvart” y “arab’ah”. El primero era empleado en la evaluación de perlas, y el otro al contar dátiles, camellos, ovejas, etc.
Pitágoras consideraba el número como la esencia de todas las cosas.
Aristóteles decía: “El número es el movimiento acelerado o retardado.”
Para muchos filósofos el concepto numérico se presenta como “la ciencia del tiempo absoluto.”[104]
El número puede, también, ser definido como la repetición sucesiva de la unidad[105].
Muchas son las definiciones formuladas sobre el concepto de número. Sin embargo, ninguna de ellas satisface al espíritu del matemático. Citaré seis de esas definiciones:
1. Número es la expresión que determina una cantidad de cosas de la misma especie.
2. Número es la representación de la pluralidad.
3. Número es la pluralidad medida con la unidad.
4. Número es el resultado de la medida de una magnitud.
5. Número es una colección de objetos de cuya naturaleza hacemos abstracción.
6. Número es un símbolo creado por el espíritu humano para caracterizar los diferentes estados de una verdad científica. [106]
Será preferible, señora, no interesarnos por la definición rigurosa de un número, pues tal concepto no parece tener definición. [107]
¿Cuál es el origen del número?
Siendo el número un concepto de relación, es bien claro que el número surgió de una comparación entre un grupo de objetos y uno de esos objetos aislados. Caminando por el desierto, el beduino ve una caravana de camellos. ¿Cuántos son? Para definir ese “cuántos”, debe emplear los números. El número será, pues, la pluralidad definida bajo la forma de una palabra o de un símbolo.
Las notaciones simbólicas empleadas por los matemáticos han sufrido profundas modificaciones a través de los siglos. La figura adjunta representa una ecuación algebraica escrita por los sabios egipcios dos o tres milenios antes de Cristo. Esa ecuación, en símbolos actuales, es la siguiente:
x/2 + x/4 + x = 10
El primer signo de la izquierda indica “mitad de x”.
Para llegar a ese resultado precisa el hombre poner en ejercicio cierta actividad, esto es, precisa contar.Al contar relaciona cada conjunto con un determinado símbolo:
uno, dos, tres…
o sea, establece una correspondencia entre la serie numérica y los objetos del conjunto que procura contar.
Para la representación de un número cualquiera con pocos signos, era necesario inventar un sistema de numeración.
El más antiguo sistema de numeración es el quinario, en el cual las unidades se agrupan de cinco en cinco.
En el primitivo sistema quinario el número de discos arriba indicado sería 32.
Una vez contadas cinco unidades obteníamos una colección llamada quina. Así 8 unidades sería una quina más 3, y escribiríamos 13. Es más importante decir que en este sistema el segundo guarismo de la izquierda valía 5 veces más que si estuviese en el primer lugar. Los matemáticos dicen, por consiguiente, que la base de ese sistema era 5.Se encuentran vestigios de dicho sistema en los poemas antiguos.
Otro de los sistemas empleados, fue el de base 20, por el cual se designa al número ochenta por la expresión cuatro veintes. [108]
Los árabes usaron guarismos que diferían bastante de los actuales. Así podemos observar que el cinco árabe era un pequeño círculo, mientras que el cero se representaba por un punto.
Surgió después, señora, el sistema de base 10, que se prestaba más para expresar grandes cantidades. El origen de ese sistema se explica por el número de dedos de la mano. Algunos pueblos, sin embargo, demostraban preferencia por un sistema que tenía por base el número 12 (una docena). La docena presenta sobre la decena una gran ventaja: el número 12 tiene más divisores que el número 10. [109]
Las de la figura son las diversas formas presentadas por los números egipcios desde 1 hasta 9. “En la numeración escrita de los egipcios el 10 era representado por una herradura; 100 por una hoja de palmera enrollada en espiral: 1000 por una flor de loto, símbolo del Nilo, a quien debían la fertilidad del suelo; 10000 por un indicador; 100000 por un “embrión de rana”, porque las ranas eran encontradas en gran cantidad, en la primera faz de su vida, en el lodo que las aguas del Nilo arrastraban durante el período de las inundaciones.”
El sistema decimal fue, no obstante, universalmente adoptado. Desde el tuareg que cuenta con los dedos hasta el matemático que maneja instrumentos de cálculo, todos contamos de 10 en 10. Dadas las divergencias profundas entre los pueblos, semejante universalidad es sorprendente; no puede jactarse de lo mismo ninguna religión, código moral, forma de gobierno, sistema económico, principio filosófico o artístico, lenguaje, ni alfabeto alguno. Contar es uno de los pocos tópicos en torno al cual los hombres no divergen, pues lo consideran lógico y natural.
Difícilmente encontraremos un matemático que sepa leer y calcular la expresión que aparece representada en la figura de arriba. Dicha expresión – afirma Rouse Ball – fue incluida, junto con muchas otras, en una obra notable de Nicolás Churquet publicada en 1854. Vemos abajo la misma expresión por medio de notaciones modernas.
Nárrase que un pastor, que necesitaba estar seguro que tenía todas sus ovejas al anochecer, tuvo que exceder, al contar su rebaño, a la primera decena. Contaba las ovejas que desfilaban por frente a él, doblando un dedo por cada una, y cuando tenía doblados diez dedos, apartaba un guijarro plano. Terminada la tarea, los guijarros [110] representaban el número de “manos llenas” (decenas), de ovejas del rebaño. Al día siguiente podía rehacer la cuenta comparando los montones de guijarros.
Luego se le ocurrió a algún cerebro propenso a lo abstracto, que se podía aplicar aquel proceso a otras cosas útiles, como los dátiles, el trigo, los días, las distancias y las estrellas. Y haciendo marcas, en lugar de apartar guijarros, se creó el sistema de numeración escrita.
Todos los pueblos adoptaron en su lenguaje hablado, el sistema decimal; los otros sistemas fueron abolidos y relegados. Mas, la adaptación de tal sistema a la numeración escrita sólo se hizo muy lentamente.
Fue necesario el esfuerzo de varios siglos para que la humanidad descubriese una solución perfecta al problema de la representación gráfica de los números.
Para representarlos, imaginó el hombre caracteres especiales llamados guarismos, representando cada uno de esos signos los vocablos: uno,dos, tres, cuatro, cinco, seis, siete, ocho y nueve. Otros signos auxiliares, tales como d, c, m, etc., indicaban que el guarismo que acompañaba representaba decena, centena, millar, etc. Así, un matemático antiguo representaba el número 9765 por la notación 9m, 7c, 6d, 5. Los fenicios, que fueron los grandes comerciantes de la antigüedad, en vez de letras usaban acentos:
9’’’ 7’’ 6’ 5.
Los griegos, al principio no adoptaron ese interesante sistema. A cada letra del alfabeto, acompañada de un acento, le atribuían un valor; así la primera letra (alfa) era el 1; la segunda letra (beta) era el 2; la tercera letra (gama) era el 3, y así por consiguiente, hasta el número 19. El 6 era la excepción: ese número se representaba por un signo especial (estigma).Combinando, después, las letras dos a dos, representaban 20, 21, 22, etc.
Son interesantes las notaciones matemáticas encontradas en el papiro Rhind escrito por el sacerdote egipcio Ashmesu – o mejor Ahmés – “hijo de un rey llamado Ra – a –us”. Los egiptólogos, después de largos y cuidadosos estudios, descubrieron que el trabajo del sabio Ahmés fue hecho cerca de 20 siglos antes de Cristo.
El número 4004 era representado, en el sistema griego, por dos guarismos; el número 2022 por tres guarismos diferentes; el número 3333 era representado por 4 guarismos que diferían por completo unos de otros.Prueba de menor imaginación dieron los romanos, conformándose con tres caracteres, I, V y X, para formar los diez primeros números, y con los caracteres L (cincuenta), C (cien), D (quinientos), M (mil), que combinaban con los primeros.
Los números escritos en guarismos romanos eran así de una complicación absurda, y se prestaban tan mal a las operaciones elementales de la Aritmética, que una simple adición era un tormento.
Con la escritura rúnica, la adición podía, en realidad, hacerse en el papel (antes en el papiro, porque no se conocía el papel), disponiendo los números, unos debajo de otros, de tal suerte que los guarismos con el mismo valor formasen columna, lo que obligaba a mantener la distancia entre los guarismos para tener en cuenta los órdenes que faltaran.
Estaba la ciencia de los números en este estado hace unos cuatrocientos años, cuando un hindú, de quien la historia no conservó el nombre, imaginó emplear un carácter especial, el cero [111], para indicar, con un número escrito, la ausencia de toda unidad de determinado orden. Gracias a esta invención, todos los signos, índices y letras, volviéronse inútiles; quedaron solamente los nueve guarismos y el cero. La posibilidad de escribir un número cualquiera por medio de diez caracteres fue el primer milagro del cero.
Los geómetras árabes se apoderaron de la invención del hindú y notaron que, agregando un cero a la derecha de un número, se elevaba, automáticamente, el orden decimal a que pertenecían sus diferentes guarismos. Veremos en la próxima clase (¡Si Alah lo quiere!) cuáles son las principales operaciones o transformaciones que podemos efectuar con los números y las propiedades que éstos presentan.
Calló Beremís. Había terminado la segunda clase de Matemática.
Oímos entonces, entonados por la voz cristalina de Telassim, los siguientes versos:
“Dadme ¡oh Dios! Fuerzas para volver mi amor fértil y útil.
Dadme fuerzas para no despreciar jamás al pobre ni doblar la rodilla ante el poder insolente.
Dadme fuerzas para elevar mi espíritu bien alto sobre las futilezas de todos los días.
Dadme fuerzas para que me humille con amor delante de ti.
No soy más que un jirón de nube de otoño, vagando por el cielo, ¡oh, mi Sol glorioso!
Si es tu deseo y gusto, tómalo, píntalo de mil colores, irísalo de oro, hazlo fluctuar al viento, espárcelo por el cielo en múltiples maravillas
Y después, si fuera tu deseo terminar, por la noche, ese juego, desaparecería desvaneciéndome en la tiniebla, o tal vez en una sonrisa de alborada, transparente de frescura y de pureza.”
- Es admirable –balbuceó a mi lado, el gramático Doreid.
- Sí -asentí-. La Matemática es admirable.
- ¡Qué Matemática ni que nada! –protestó mi poco oportuno vecino-. No vine aquí para oír esa historia inacabable de números y guarismos. Eso no me interesa. Califiqué de admirable la voz de Telassim.
Y como quedase asombrado delante de aquella ruda franqueza, él añadió:
- Siempre pensé que al permanecer en esta sala, durante la clase, pudiese ver el rostro de la joven. Dicen que es hermosa como la cuarta luna de Ramadán.
Y se levantó canturreando bajito:
“Si no tienes ganas de llenar tu cántaro, si prefieres dejarlo flotando en el agua, ven, ven a sentar tu pureza en mi lago.
La ladera está verde, y las flores de mi campo son tantas que no pueden contarse. Se te irán tus pensamientos por tus ojos negros, como pájaros que vuelan de sus nidos, y tu velo se te caerá a tus pies.
Ven, ven a mi lago, si no tienes ganas de llenar tu cántaro.
Si, harta de tus otros juegos, quieres jugar con el agua, ven, ven a mi lago.
Deja tu manto azul en la orilla, que el agua azul te esconderá. Y las olas se pondrán de puntillas por besar tu cuello y suspirar en los oídos.
Ven, ven a mi lago, si quieres jugar con el agua.
Si te has vuelto loca y quieres morir, ven, ven a mi lago.
Mi lago es frío y no tiene fondo; oscuro como un sueño sin sueños. Allá abajo, noches y días son iguales, y toda canción es silencio.
Ven, ven a mi lago, si te has vuelto loca y quieres morir.”[112]
Dejamos con melancolía y quieta la sala llena de luz.
Noté que Beremís no tenía más en el dedo el anillo que había ganado en la posada el día de nuestra llegada. ¿Había perdido su joya predilecta?
La esclava circasiana miraba vigilante, como si temiese el sortilegio de algún “djin” invisible.
Capítulo 21
En el cual comienzo a copiar libros de Medicina. Progreso de la alumna invisible. Beremís es llamado para resolver un problema. La mitad de la incógnita de la vida. El rey Mazin y las prisiones de Khorazan. Un verso, un problema y una leyenda. La justicia del rey Mazin.
Por las referencias que oía de mi amigo el calculista, la “alumna invisible” habría hecho grandes progresos, en las últimas semanas, en la ciencia de Báskara. Ya conocía las cuatro operaciones con los números, los tres primeros libros de Euclides y calculaba, también, el valor de las fracciones con numerador 1, 2, ó 3. [114]
Cierto día, al caer la tarde, íbamos a comenzar nuestra modesta refección, que consistía apenas en media docena de empanadas de carnero, con cebollas, miel, harina y aceitunas, cuando oímos en la calle gran tropel de caballos y, en seguida, gritos, voces de mando e imprecaciones de soldados turcos.
Me levanté un poco asustado. ¿Qué había sucedido? Tuve la impresión que la posada era cercada por tropas y que una nueva violencia iba a ser llevada a cabo por orden del intolerante Jefe de Policía.
La inesperada algazara no impresionó a Beremís. Completamente ajeno a los acontecimientos de la calle, continuó, como antes, trazando figuras geométricas sobre un gran tablero de madera. ¡Qué hombre extraordinario! Ni las agitaciones más grandes, ni los peligros, ni las amenazas de los poderosos, conseguían desviarlo de sus estudios matemáticos. Si Asrail, el Ángel de la Muerte, surgiese allí, de repente, trayendo en la hoja de su “kangiar” la sentencia de lo Irremediable, continuaría él, impasible, trazando curvas y ángulos, y estudiando las propiedades de las figuras y de las relaciones entre los números.
El pequeño aposento en que nos hallábamos fue invadido por el viejo Salim, a quien acompañaban dos esclavos negros y un camellero. Todos se mostraban asustadísimos, como si algo grave hubiera sucedido.
- ¡Por Alah! –grité, impaciente-. No molesten a nuestro calculista. ¿Qué algazara es ésta? ¿Hay nuevos disturbios en Bagdad? ¿Desapareció la mezquita de Solimán?
- Señor –balbuceó el viejo Salim con voz trémula de susto-. Una escolta… Una escolta de soldados turcos acaba de llegar.
- ¡Por el santo nombre de Mahoma! ¿Qué escolta es esa, Salim?
- Es la escolta del poderoso gran visir Ibraim Maluf-el-Barad (¡Que Alah lo llene de bondades!). Los soldados vienen con orden de llevar inmediatamente al calculista Beremís Samir.
- ¡Para qué tanto escándalo, chacales! –bramé, excitado-. Eso carece de importancia. Naturalmente el visir, nuestro buen amigo y protector, desea resolver, con urgencia, un problema de Matemática, y necesita del valioso concurso de nuestro sabio calculista.
Mis previsiones fueron tan acertadas como los más perfectos cálculos de Beremís.
Momentos después, llevados por oficiales de la escolta, llegamos al palacio del visir Maluf.
Encontramos al poderoso ministro en la fastuosa sala de audiencias, acompañado de tres auxiliares de confianza. En la mano tenía una hoja llena de números y de cálculos.
¿Qué nuevo problema sería aquel que perturbara tan profundamente el espíritu del digno auxiliar del califa?
- El caso es grave, calculista –comenzó el visir, dirigiéndose a Beremís-. Me encuentro, en este momento, atribulado frente a uno de los más complicados problemas que se me han presentado en mi vida. Quiero informaros minuciosamente de los antecedentes del caso, pues solo con vuestra ayuda podremos hallar, tal vez, una solución.
Contó el visir lo siguiente:
- Anteanoche, pocas horas antes que nuestro glorioso califa Al-Motacen, Emir de los Creyentes, partiera para Basora (donde quedará por tres semanas), hubo un incendio en la prisión. Durante muchas horas la violencia del fuego amenazó destruirlo todo. Los detenidos, encerrados en sus celdas, sufrieron gran suplicio, torturados por angustias indecibles. Frente a ese hecho, nuestro generoso soberano ordenó fuera reducida a la mitad la pena de todos los condenados. Al principio no dimos importancia alguna al caso, pues parecía muy simple ordenar se cumpliera, con todo rigor, la sentencia del rey. Al día siguiente, sin embargo, cuando la caravana del Príncipe de los Creyentes ya estaba lejos, verificamos que esa resolución de última hora involucraba un problema extremadamente delicado, y cuya solución perfecta parecía imposible.
- Entre los detenidos beneficiados por la ley –prosiguió el ministro- hay un contrabandista de Basora, llamado Sanadique, condenado hace cuatro años a prisión perpetua. La condena de ese hombre debe ser reducida a la mitad. Ahora bien; como fue condenado a prisión por toda su vida, se deduce que, en virtud de la ley, deberá ser perdonado de la mitad de la pena, o mejor aún, de la mitad del tiempo que le resta vivir. Si llamamos “x” a la duración desconocida de su vida, ¿cómo dividir por dos un período de tiempo que ignoramos? ¿Cómo calcular la mitad de la incógnita de los años “ x” de su vida?
Después de pensar durante unos minutos, Beremís respondió:
- Ese problema me parece en extremo delicado, por tratarse de un caso de Matemática pura y de interpretación de la ley. Es un caso que interesa a la justicia de los hombres y a la Verdad de los números. No puedo discutirlo, con los poderosos recursos del Álgebra y del Análisis, antes de visitar la celda en que se halla condenado Sanadique. Es posible que la “x” de su vida esté calculada por el Destino, en la pared de la celda del propio condenado.
- Juzgo infinitamente extraño vuestro parecer –observó el visir- . No cabe en mi cabeza la relación que pueda existir entre las blasfemias con que los locos y los condenados adornan los muros de las prisiones, y la resolución algebraica de tan delicado problema.
- Sidi –interrumpió Beremís-: se encuentran, muchas veces, en las paredes de las prisiones, leyendas interesantes, fórmulas, versos e inscripciones que iluminan el espíritu y nos orientan hacia pensamientos de bondad y clemencia. Cuéntase que cierta vez, el rey Mazin, señor de la rica provincia de Khorazan, fue informado que un presidiario hindú había escrito palabras mágicas en las paredes de su celda. El rey Mazin llamó a un escriba inteligente y hábil, y le ordenó copiase todas las letras, figuras, versos o números que encontrase en las paredes sombrías de la prisión. Muchas semanas empleó el escriba para cumplir, íntegramente, la orden extravagante del rey. Al final, después de pacientes esfuerzos, llevó al soberano decenas de hojas llenas de símbolos, palabras ininteligibles, figuras disparatadas, blasfemias de locos y números sin significado. ¿Cómo traducir o descifrar aquellas páginas repletas de cosas incomprensibles? Uno de los sabios del país, consultado por el monarca, dijo: “Rey, esas hojas contienen maldiciones, blasfemias, herejías, palabras cabalísticas, versos, leyendas y hasta un problema de Matemática con cálculos y figuras”.
Respondió el rey: “Las maldiciones, blasfemias y herejías no calman la curiosidad que llena mi espíritu. Las palabras cabalísticas me dejan indiferente; no creo en el poder oculto de las letras ni en la fuerza misteriosa de los símbolos humanos. Me interesa, sin embargo, conocer el verso, el problema y la leyenda, pues son producciones que ennoblecen al hombre y pueden traer consuelo al afligido, enseñanza al ignorante y advertencia al poderoso”.
Ante el pedido del monarca, dijo el “ulema”:
- Estos son los versos escritos por uno de los condenados:
No hables de tu felicidad a alguien menos feliz que tú.
Cuando no se tiene lo que se ama, es preciso amar lo que se tiene. [115]
He aquí ahora el problema escrito con carbón en la celda de un condenado:
Colocar 10 soldados en cinco filas teniendo cuatro soldados en cada fila.
Ese problema, aparentemente imposible, tiene una solución muy simple indicada en la figura, en la cual aparecen cinco filas con cuatro soldados en cada una.
A continuación el “ulema”, para satisfacer el pedido del rey, dio lectura a la siguiente leyenda:
“Cuéntase que el joven Tzu-Chag, se dirigió un día al gran Confucio y le preguntó:
- ¿Cuántas veces, ¡oh iluminado filósofo!, debe un juez reflexionar antes de sentenciar?
Respondió Confucio:
- Una vez hoy; diez veces mañana.
Asombróse el príncipe Tzu-Chang al oír las palabras del sabio. El concepto era oscuro y enigmático.
- Una vez será suficiente –aclaró con paciencia el Maestro- cuando el juez, por el examen de la causa, concluye perdonado. Diez veces, sin embargo, deberá el magistrado pensar, siempre que se sienta inclinado a librar sentencia condenatoria.
Y concluyó, con su incomparable sabiduría:
- Erra, por cierto, gravemente, aquel quien hesita en perdonar; erra, no obstante, mucho más aún, a los ojos de Dios, aquel que condena sin hesitar.”
La figura que ilustra está página indica la única solución que puede darse al siguiente problema: “Colocar 10 soldados en 5 filas de 4 soldados por fila”
Se admiró el rey Mazin al saber que había, e las húmedas paredes de los calabozos subterráneos, escritas por los míseros presos, tanta cosa llena de belleza y curiosidad. Naturalmente que en medio de los que pasaban sus días llenos de amargura en el fondo de las celdas, había muchos cultos e inteligentes. Determinó, pues, el rey, que fueran revisados todos los procesos y juicios, y verificó que innumerables sentencias eran evidentemente injustas. Y así, gracias a la libertad muchos inocentes y reparados decenas de errores judiciales.- Todo eso puede ser muy interesante –dijo el visir Maluf-. Peor es muy posible que en las prisiones de Bagdad no se pueda encontrar figura geométrica, versos o leyenda morales. Quiero ver, sin embargo, el resultado a que pretendéis llegar. Permitiré, por tanto, vuestra visita a la prisión.
Capítulo 22
En el cual visitamos los prisioneros de Bagdad. Cómo resolvió Beremís el problema de la mitad de la “x” de la vida. El instante de tiempo. La libertad condicional. Beremís aclara los fundamentos de una sentencia.
Nadie podría imaginar la vida de sufrimientos y miserias de aquellos que eran encerrados en el fondo de las mazmorras de la gloriosa ciudad árabe.
A la celda en que se hallaba el infeliz Sanadique, que desde ya hacía pensar en cosas espeluznantes, trágicas y tremendas, llegamos guiados por el carcelero, y auxiliados por dos guardias.
Un esclavo nubio, casi un gigante, conducía una gran antorcha, cuya luz nos permitía observar todos los rincones de la prisión.
Después de recorrer un corredor estrecho, que apenas daba paso a un hombre, descendimos por una escalera húmeda y oscura. En el fondo del subterráneo se hallaba el pequeño calabozo donde fuera encerrado Sanadique. En él no entraba ni la más tenue claridad. No se podía respirar el aire pesado y fétido sin sentir náuseas y vahídos. El suelo estaba cubierto de una capa de lodo putrefacto y no había, entre las cuatro paredes, ninguna cosa que pudiese servirse el condenado para descansar.
A la luz de la antorcha que el hercúleo nubio levantaba, vimos al desventurado Sanadique, semidesnudo, la barba crecida y enmarañada, los cabellos en desaliño cayéndole sobre los hombros, sentado sobre una losa, las manos y los pies sujetos a cadenas de hierro.
Beremís observó en silencio, con vivo interés, al desventurado Sanadique. Era increíble que un hombre pudiese resistir cuatro años en aquella inhumana y dolorosa situación.
Las paredes de la celda llenas de manchas de humedad, se hallaban repletas de leyendas y figuras –extraños indicios de muchas generaciones de infelices condenados-. Beremís examinó, leyó y tradujo con minucioso cuidado todo aquello, deteniéndose, de vez en cuando, para hacer cálculos que nos parecían largos y laboriosos. ¿Cómo podría el calculista, entre las maldiciones y blasfemias que los condenados suelen escribir, descubrir la mitad de la “x” de la vida?
Grande fue la sensación de alivio que sentí al dejar la sombría prisión, donde los detenidos eran tan cruelmente tratados. Al llegar de vuelta a la suntuosa sala de audiencias, nos encontramos con el visir Maluf rodeado de cortesanos, secretarios, jefes y “ulemas” de la Corte. Esperaban todos la llegada de Beremís, pues querían conocer la fórmula que emplearía el calculista para resolver el problema de la mitad de prisión perpetua.
- ¡Estamos esperándote, calculista! –dijo el visir-. Espero que presentes, sin más demoras, la solución de este gran problema. Tenemos la mayor urgencia en hacer cumplir la sentencia de nuestro gran Emir.
Al oír esa orden, Beremís se inclinó respetuoso, hizo el acostumbrado “zalam” y habló así:
- El contrabandista Sanadique, de Basora, apresado hace cuatro años en la frontera, fue condenado a prisión perpetua. Esa pena acaba, sin embargo, de ser reducida a la mitad por justa y sabia sentencia de nuestro glorioso califa AL-Motacen, Comendador de los Creyentes, sombra de Alah en la Tierra.
Designemos por x el período de Sanadique, período que comienza en el momento en que fue apresado y condenado hasta el término de sus días. Sanadique fue, por lo tanto, condenado a x años de prisión, esto es, a prisión por toda la vida. Ahora, en virtud de la regia sentencia, esa pena deberá reducirse a la mitad. Si dividimos el tiempo x en varios períodos, a cada período de prisión debe corresponder igual período de libertad.
- Completamente cierto –dijo el visir-. Comprendo perfectamente su razonamiento.
- Ahora bien; como Sanadique ya estuvo preso durante cuatro años, es claro que deberá quedar en libertad durante igual período, esto es, durante cuatro años.
En efecto. Imaginemos que un mago genial pudiese prever el número exacto de años de vida de Sanadique y nos dijese ahora: “Ese hombre, en el momento en que fue puesto preso, tenía apenas 8 años de vida.” En ese caso tendríamos que x es igual a 8, o sea, que Sanadique habría sido condenado a 8 años de prisión, pena que ahora quedaría reducida a 4 años. Como Sanadique ya está preso desde hace 4 años, ya cumplió el total de la pena y debe ser considerado libre. Si el contrabandista, por determinación del Destino, hubiera de vivir más de 8 años, su vida x (mayor que 8) podrá ser descompuesta en tres períodos: uno de 4 años de prisión (ya cumplido), otro de 4 años de libertad, y un tercero que deberá ser dividido en dos partes iguales (prisión y libertad). Es fácil, pues, sacar en conclusión que, para cualquier valor de x (desconocido), el preso deberá ser puesto en libertad inmediatamente, quedando libre por cuatro años, pues tiene perfecto derecho a ello, como ya demostré, de acuerdo con la ley.
Al final de ese plazo, o mejor, terminado ese período, deberá volver a la prisión y quedar prisionero por un tiempo igual a la mitad del resto de su vida.[116]
Sería conveniente, tal vez, encarcelarlo durante un año y concederle la libertad durante el año siguiente; año libre y pasaría, de ese modo, la mitad de su vida en libertad, conforme manda la sentencia del rey.
Esa solución, sin embargo, solo sería verdadera si el condenado muriese en el último día de uno de sus períodos de libertad.
En efecto:
Imaginemos que Sanadique, después de pasar un año en la prisión, fuese libertado y muriese, por ejemplo, en el cuarto mes de libertad. De esa parte de su vida (un año y cuatro meses) habría pasado: un año preso y cuatro meses en libertad. ¿No es así? Hubo error en el cálculo. Su pena no fue reducida a la mitad.
Podrá parecer que la solución de este caso, consistiría, finalmente, en prender a Sanadique un día para soltarlo al día siguiente, concediéndole igual período de libertad, y proceder así hasta el término de sus días.
Tal solución no será, con todo, rigurosamente cierta, pues Sanadique -como es fácil comprender- puede resultar perjudicado en muchas horas de libertad. Bastaría para eso que él muriera horas después de un día de prisión.
Detener a condenado durante una hora y soltarlo a la siguiente, dejándolo en libertad durante una hora, y así sucesivamente hasta la última hora de vida del condenado sería la solución correcta, si Sanadique muriera en el último minuto de una hora de libertad. De lo contrario su pena no habría sido reducida a la mitad.
La solución matemáticamente exacta consistirá en lo siguiente:
Prender a Sanadique durante un instante de tiempo y soltarlo al siguiente. Es necesario, sin embargo, que el tiempo que esté preso (el instante) sea infinitamente pequeño, esto es, indivisible. Lo mismo ha de suceder con el período de libertad siguiente.
En la realidad, dicha solución es imposible.
¿Cómo prender a un hombre en un instante indivisible, y soltarlo al instante siguiente? Debemos, por tanto, apartarla de nuestros pensamientos. Sólo veo ¡oh visir! Una forma de resolver el problema: Sanadique será puesto en libertad condicional, bajo la vigilancia de la ley. Es esa la única manera de detener y libertar un hombre al mismo tiempo.
Ordenó el gran visir que fuese cumplida la sugestión del calculista, y el infeliz Sanadique fue, en el mismo día “libertado condicionalmente” –fórmula que los jurisconsultos árabes adoptaron después, frecuentemente, en sus sabias sentencias.
Al día siguiente le pregunté qué datos o elementos de cálculo consiguiera hallar él, en las paredes de la prisión, durante la célebre visita, que lo llevaran a dar tan original solución al problema del condenado. Respondió el calculista:
- Sólo quien ya estuvo, por unos momentos siquiera, entre los muros tenebrosos de una mazmorra, sabe resolver esos problemas en que los guarismos son partes terribles de la desgracia humana.
Capítulo 23
En el cual recibimos una honrosa visita. Palabras del príncipe Cluzir Schá. Beremís resuelve un problema. Las perlas del Rajá. Un número cabalístico. Queda resuelta nuestra partida para la India.
Beremís, por la mañana, recibió inesperadamente la visita honrosa del príncipe Cluzir Schá.
Cuando la lujosa comitiva desfiló por las calles, los balcones y terrazas se llenaron de curiosos. Mujeres, viejos y niños admiraban mudos y asombrados el maravilloso espectáculo.
Precediendo los estandartes con el escudo del príncipe (elefante blanco sobre fondo azul). Venían, al frente, cerca de treinta caballeros, montados en soberbios corceles árabes, con arreos repujados y gualdrapas de terciopelo bordado de plata. Lucían albos mantos y túnicas, y largas cimitarras sujetas con arreos de cuero lustrado, pendían a un costado; en sus cabezas, blancos turbantes con yelmos metálicos, relucían al sol. Después seguían varios arqueros y batidores, todos a caballo.
Y cerrando el cortejo apareció el poderoso maharajá, acompañado de dos secretarios, tres médicos y diez pajes. El príncipe vestía una túnica escarlata, toda adornada con hilos de perlas. En el turbante, de una riqueza fastuosa, centelleaban innumerables zafiros y rubíes.
Cuando el viejo Salim vio llegar a su posada, aquella majestuosa comitiva, le dio como un ataque de locura y, tirándose al suelo, comenzó a gritar:
- ¡Men ein! ¡Men ein! [117]
Mandé que un aguatero arrastrase al alucinado amigo al fondo del patio, hasta que la calma volviese a su conturbado espíritu.
La sala de la posada era pequeña para dar cabida a los ilustres visitantes. Beremís, maravillado de la honrosa visita, descendió al patio a recibirlos.
El príncipe Cluzir, al llegar, saludó al calculista con un amistoso “zalam”, y le dijo:
- El peor sabio es aquel que frecuenta a los ricos; el mayor rico es aquel que frecuenta a los sabios. [118]
- Bien sé, señor – respondió Beremís- que vuestras palabras son inspiradas por el más grande sentimiento de bondad. La pequeña e insignificante parte de ciencia que conseguí adquirir, desparece ante la generosidad infinita de vuestro corazón.
- Mi visita, calculista –interrumpió el príncipe- se debe más al egoísmo que al interés en la ciencia. Después que tuve el placer de oírlo, en casa del poeta Iezid, pensé en ofrecerle algún cargo de importancia en mi Corte. Deseo nombrarlo mi secretario o director del Observatorio de Delhi. ¿Acepta? Partiremos dentro de pocas semanas para la Meca y de allá para la India.
- Desgraciadamente, ¡oh príncipe generoso! –respondió Beremís-, no puedo ausentarme ahora de Bagdad. Sólo podré irme de aquí después que la hija del ilustre Iezid haya aprendido Matemática.
Sonrió el maharajá y respondió:
- Se el motivo de su negativa frente a ese compromiso, y creo que pronto llegaremos a un acuerdo. El sheik Iezid me ha dicho que la joven Telassim, dado los progresos que ha hecho, dentro de pocos meses estará en condiciones de enseñar a los “ulemas” el famoso “ problema de las perlas del Rajá”.
- Yo mucho desearía –prosiguió el príncipe- conocer el complicado problema que viene desafiando la sagacidad de os algebristas y que se refiere, sin duda, a uno de mis gloriosos antepasados.
Beremís respondió:
- Trátase más de una curiosidad aritmética que de un problema, y este es su enunciado:
“Un rajá dejó a sus hijas cierto número de perlas y ordenó que el reparto se hiciese del siguiente modo: a la hija mayor correspondería una perla más un séptimo de las que quedasen; la segunda tomaría dos perlas y un séptimo de las restantes; la tercera recibiría tres perlas y un séptimo de las que quedasen. Y así sucesivamente, para las restantes hijas.
Las hijas más jóvenes presentaron su queja a un juez, alegando que por ese sistema complicado ellas serían fatalmente perjudicadas.
El juez –dice la tradición-, que era hábil en la resolución de problemas, respondió rápidamente que las demandantes estaban equivocadas, y que la división propuesta por el Rajá era justa y perfecta.
El juez tenía razón. Hecha la división, cada una de las hermanas recibió el mismo número de perlas.”
Se pregunta: ¿Cuál es el número de perlas? ¿Cuántas las hijas del Rajá?
La solución es muy sencilla:
Las perlas eran 36 y debían repartirse entre 6 personas.
La primera sacó una perla y, además, un séptimo de 35, o sea 5; luego, sacó 6 perlas y dejó 30.
La segunda, de las 30 que encontró sacó 2 y, además, un séptimo de 28, que es 4; luego, sacó 6 y dejó 24.
La tercera, de las 24 que encontró, sacó 3 y, además, un séptimo de 21, que es 3 y, además, un séptimo de 21, o sea 3, por lo tanto, 56 y dejó 18.
Solución gráfica del famoso problema de las “perlas del Rajá”.
La cuarta, de las 18 que encontró, sacó 4 y, además, un séptimo de 14, o sea 2. Recibió, también, 6 perlas.La quinta encontró 12 perlas; de esas 12 sacó 5 y, además, un séptimo de 7, o sea 1; luego sacó 6.
A la hija más joven le tocó, por fin, las 6 perlas restantes.
Beremís concluyó:
- Como veis, el problema, si bien ingenioso, nada tiene de difícil. Se llega a la solución sin artificios ni sutilezas de raciocinio. [119]
En ese momento llamó la tensión del príncipe Cluzir Schá, un número que se hallaba escrito cinco veces en la pared de la habitación.
Era el número 142857.
- ¿Qué significado tiene ese número? –preguntó.
- Se trata de uno de los números más curiosos en Matemática –respondió Beremís-. Presenta, con respecto a sus múltiplos, coincidencias interesantes:
Si lo multiplicamos por 2, el producto será:
142.857 x 2 = 285.714
Vemos que los guarismos que constituyen el producto son los mismos del número dado, pero en otro dueto son los mismos del número dado, pero en otro orden. El 14, que se hallaba a la izquierda, se encuentra ahora a la derecha.Efectuemos el producto del número 142857 por 3:
142.857 X 3 = 428.571
Se observa aquí la misma singularidad: los guarismos del producto son los mismos del número, pero alterados, apenas, en el orden. El 1, que se hallaba a la izquierda, pasó a la derecha; los demás permanecieron en el orden primitivo.Lo mismo ocurre cuando el número se multiplica por 4:
142.857 X 4 = 571.428
Veamos ahora lo que ocurre en el caso de la multiplicación por 5:142.857 X 5 = 714.285
El guarismo 7 se trasladó de la derecha para la izquierda. Los restantes permanecieron en sus lugares.Observemos la multiplicación por 6:
142.857 X 6 = 857.142
Hecho el producto, se nota que sólo el grupo 142 permutó su posición con el 857.Al llegar al factor 7 nos llama la atención otra particularidad. El número 142.857, multiplicado por 7, da como producto el número:
999.999
formado por seis nueves.Si lo multiplicamos por 8, el producto será:
142857 x 8 = 1.142.856
Todas las cifras aparecen en el producto, a excepción del 7. El 7 del número primitivo fue descompuesto en dos partes: 6 y 1. El guarismo 6 quedó a la derecha y el 1 fue para la izquierda a completar el producto.Veamos que sucede cuando lo multiplicamos por nueve:
142.857 x 9 = 1.285.713
Observando con detención ese resultado, vemos que el único guarismo que no figura es el 4. ¿Qué ha pasado con él? Aparece descompuesto en dos partes, el 1 y el 3, colocados en los extremos del producto.Del mismo modo podríamos verificar las rarezas que presenta el número 142.857, multiplicándolo por 11, 12, 13, 15, 16, 18, etc.
Es por eso, que el número 142.857 se incluye entre los números cabalísticos de la Matemática. Enseñóme el derviche No-Elin…
- ¡No-Elin! –repitió, lleno de vivo júbilo, el príncipe Cluzir Schá-. ¿Es posible que haya conocido a ese sabio?
- Lo conocí, y muy bien, Príncipe –respondió Beremís-. Con él aprendí todos los principios que hoy aplico a mis investigaciones matemáticas.
- Pues, el gran No-Elin –explicó el hindú- era amigo de mi padre. Cierta vez, vencido por la pena de haber perdido un hijo en combate, durante una guerra injusta y cruel, se ausentó de la ciudad y nunca más fue visto. Hice varias investigaciones para encontrarlo, mas hasta hoy no había obtenido la menor indicación sobre su paradero. Llegué hasta pensar que hubiese perecido en el desierto, devorado por las panteras. ¿Sabrá, acaso, decirme dónde podré encontrar a No-Elin?
Beremís respondió:
- Cuando partí para Bagdad, dejé al sabio No-Elin en Khoy, Persia, recomendado a tres amigos.
- Pues, luego que yo regrese de la Meca, iremos a la ciudad de Khoy a buscar a ese gran “ulema” – respondió el príncipe-. Quiero llevarlo a mi palacio. ¿Podrá usted auxiliarme en esa magna empresa, calculista?
- ¡Señor! –respondió Beremís-. Si es para prestar auxilio y hacer justicia a aquel que fue mi guía y maestro, pronto estoy para acompañaros, si fuese preciso, hasta la India.
Y así, por causa del 142.857, quedó resuelto nuestro viaje a la India, a la tierra de los Rajás.
¡Dicho número es realmente cabalístico!
Capítulo 24
En el cual Beremís, por medio de fórmulas, calcula la belleza de una joven. La división áurea. Cómo se determina, sin error, el valor numérico de la Belleza.
Había yo observado que Hassan se tornaba día a día uno de los más asiduos concurrentes del “Patito Dorado”. Raro era el día en que el guapo capitán de policía no se presentara a hacer una consulta al calculista.
Hoy, al regresar de la mezquita, encontré a Muarique en animada conversación con Beremís. Se trataba de la resolución de un nuevo problema, que parecía muy complicado, pues vi al talentoso matemático, indeciso, analizando figuras y aplicando fórmulas sin llegar a un resultado satisfactorio.
Al final se retiró el turco con los guardias que lo acompañaban.
Sólo entonces pude oír la explicación, de labios de Beremís, de aquel raro interés del turco por la ciencia.
Me contó el calculista lo siguiente:
- Hassan Muarique, capitán de la guardia, resolvió casarse con una joven llamada Zaira, hija del mercader Abul Lahabe, de Basora. No quería, sin embargo, arriesgarse a pedir a la jovencita en casamiento, sin asegurarse previamente de si ella era hermosa o estaba desprovista de encantos. Ya había recurrido a todos los artificios imaginables para descubrir el rostro de Zaira, pero sin resultado. No quiso, sin embargo, guiarse únicamente por las informaciones de las viejas “catbeth” [120], ya que esas casamenteras exageran las virtudes de las novias para engañar a los pretendientes ingenuos. Ante ese inconveniente, Hassan me ha pedido lo auxiliase a resolver el problema. ¿Cómo deberá hacer para asegurarse, antes del casamiento, de la belleza de su esposa?
Hallé original aquella consulta y le dije:
- La Matemática dispone de recursos maravillosos. Con el auxilio de dicha ciencia puede el hombre calcular el peso de un camello, la altura de una torre o la belleza de una mujer. Y como él me mirase con ojos espantados, aclaré: “Sí, con el auxilio de una relación geométrica, puede el matemático determinar si una joven es hermosa o fea, es decir, si sus formas son perfectas o no. Es enteramente innecesario, para el novio, ver el rostro de su futura esposa para prevenirse contra cualquier desilusión. Basta dispones de media docena de medidas y aplicar a ellas las “fórmulas matemáticas de belleza” ”.
- Exigí –prosiguió Beremís- que Hassan obtuviese ciertas medidas del rostro de Zaira. Esas medidas, tomadas en el interior del “harem” por una “catbet”, fueron entregadas al pretendiente. Disponiendo de los datos del problema, apliqué las fórmulas, calculé las relaciones, y llegué matemáticamente al siguiente resultado: “La joven Zaira, hija del mercader ABul-Lahabe, es linda como la décima tercera hurí del Cielo de Alah”.
- Es increíble –observé- que pueda el Álgebra llegar a ese resultado. ¿Es posible saber en qué consiste esa fórmula matemática de Belleza?
- Nada más fácil –replicó Beremís-. Puedo explicar una relación curiosa, de un modo elemental y simple.
- Sí –contesta el matemático-. Existe una manera “simpática” de dividir un todo en dos partes desiguales. Veamos en qué consiste esta forma de división.
Consideremos el segmento AB dividido en dos partes desiguales.
Admitamos que esas partes desiguales representen la siguiente relación:
“El segmento total es a la parte mayor, como la parte mayor es a la parte menor.” [121]
La proposición es la siguiente:
segmento total : parte mayor = parte mayor : parte menor
Esa división corresponde a la forma simpática que pueden presentar las dos partes desiguales. Podemos formular la siguiente regla:“Para que un todo dividido en dos partes desiguales parezca hermoso desde el punto de vista de la forma, debe presentar entre la parte menor y la mayor la misma relación que entre ésta y el todo.”
Hasta hoy no se consiguió descubrir la razón de ser o “por qué” de esa belleza. Los matemáticos, que llevaran hasta muy lejos sus estudios y observaciones, exponen varios y curiosos ejemplos que constituyen elocuentes demostraciones para el principio de esa división que los romanos llamaban “divina proporción” o “división áurea”.
En el rostro femenino “matemáticamente” hermoso, la línea C de los ojos divide a la medida total AB, en media y extrema razón.
Podemos llamarla también división en media y extrema razón.Es fácil observar que el título puesto por el calígrafo en la primera página de una obra divide, en general, la medida total del libro en media y extrema razón.
La división áurea es observada, con admirable nitidez, en las fachadas de los edificios que se distinguen por la perfección de sus líneas arquitectónicas. El famoso “panteón” de París, representado en la figura, es un ejemplo notable. Siendo AB la altura del monumento, el “punto de oro” se destaca de manera inconfundible; es el punto C por el que pasa, ya sea la línea de la base del frontispicio, o el plano que corta la base de la cúpula.
Lo mismo sucede con la línea de los ojos, que divide, en las personas bien proporcionadas, la medida total del rostro en media y extrema razón. Se observa también la divina proporción en las partes en que las falanges dividen los dedos de la mano. La división en media y extrema razón se puede hallar también en la Música, en la Pintura, en la Escultura y en la Arquitectura.En la división áurea la relación entre el todo y la parte mayor, es igual, más o menos, a:
809 / 500
En las líneas principales del rostro femenino “matemáticamente hermoso” resulta constante aquella relación.Obtenidas, pues, las medidas que me parecieron necesarias, apliqué la fórmula de la divina proporción a la joven Zaira, y verifiqué que su belleza se expresaba por el número:
808/500 que difiere muy poco del valor que define la perfección. [122]
Mediante ese resultado pude afirmar al apasionado Hassan que su novia era encantadora.
- ¿Y no temes equivocarte, amigo? –observé-. La belleza femenina resulta, a veces, de ciertos detalles que la Matemática no puede apreciar. ¡Cuántas veces el encanto de la mujer resulta de la manera de sonreír, del tono de voz, de cierta delicadeza de espíritu y de mil otros pequeñísimos detalles que, en ocasiones, para los enamorados, son todo!
Beremís no respondió. Bajó la cabeza y quedó en silencio, como si estuviese preocupado por nuevas y profundas meditaciones. [123]
Capítulo 25
En el cual reaparece Tara-Tir. El epitafio de Diofanto. El problema de Hierón. Una carta de Hassan. –Los cubos de 8 y 27. La matemática y la muerte. Cómo murió Arquímedes.
Con seguridad que preparaba alguna celada contra el incauto Beremís.
Preocupado por sus estudios y problemas, no se daba cuenta el calculista del peligro que le acompañaba, como una sombra negra.
Le hablé de la siniestra presencia de Tara-Tir y el prudente aviso del sheik Iezid.
- Todos sus recelos son infundados –respondió Beremís, sin hacer caso de mi aviso-. No puedo creer en esas amenazas. Lo que me interesa en el momento es la solución completa de un problema, que constituye el epitafio del célebre geómetra griego Diofanto.
El túmulo que encierra el cadáver de Diofanto es una maravilla digna de contemplarse. Con un artificio aritmético la piedra indica su edad:
“Dios le concedió pasar la sexta parte de su vida en la niñez; un decimosegundo en la adolescencia, y después de pasada una séptima parte más de su existencia se casó; al cabo de cinco años transcurridos en un matrimonio estéril, tuvo un hijo que murió cuando apenas había alcanzado la mitad de la vida de su padre; cuatro años más, mitigando su propio dolor con el estudio de la ciencia de los números, pasó Diofanto antes de llegar al término de su existencia”. [124]
Es posible que Diofanto, preocupado en resolver los problemas indeterminados de la Aritmética, no hubiese meditado a fin de obtener la solución perfecta para el problema del rey Hierón que no aparece indicado en su obra.
- ¿Qué problema es ese? –pregunté.
Beremís relató entonces lo siguiente:
- Hierón, rey de Siracusa, mandó a sus orfebres cierta cantidad de dinero para confeccionar una corona que él deseaba ofrecer a Júpiter. Cuando el rey recibió la obra terminada, verificó que ella tenía el peso del metal suministrado, pero el color del oro le inspiró desconfianza que los orfebres hubiesen aleado plata y oro. Para aclarar esta duda consultó a Arquímedes, el gran geómetra.
Arquímedes que había verificado que el oro pierde, en el agua, 52 milésimos de su peso, y la plata, 99 milésimos, averiguó el peso de la corona sumergida en el agua y encontró que la pérdida de peso era debida en parte a cierta cantidad de plata adicionada al oro.
En el momento en que hablábamos, vino a visitarnos el capitán Hassan Muarique, jefe de guardia del sultán. El turco se había casado, diez días antes, con la Joven Zaira, y estaba contentísimo con la elección que hiciera. Siguiendo, pues, la indicación de Beremís, pidió a la jovencita en casamiento, obteniendo una esposa muy graciosa, bondadosa e inteligente.
- Nunca imaginé –dijo, después de expresar su agradecimiento- que la Matemática fuese tan prodigiosa como para llegar a poder calcular la belleza femenina.
Al notar el entusiasmo del turco, lo llevé hasta la terraza de la habitación que daba a la calle, y mientras Beremís procuraba hallar una nueva solución al problema de Diofanto, le hablé del peligro que corríamos bajo la amenaza del odio de Tara-Tir.
- Allá está él –señalé-, junto a la fuente. Los hombres que le acompañan son asesinos peligrosos. Al menor descuido, seremos apuñaleados por esos bandidos.
- ¡Qué me cuenta! –exclamó Hassan-. Yo no podía ni imaginar que tal cosa ocurriese. ¡Por Alah! Voy ahora mismo a resolver ese caso.
Volví al cuarto, y me puse a fumar tranquilo.
Una hora después recibí el siguiente recado de Hassan:
“Todo está resuelto. Los tres asesinos fueron ejecutados sumariamente. Tara-Tir recibió 8 garrotazos, pagó una multa de 27 sequíes de oro y fue intimado a abandonar la ciudad.”
Mostré la carta de Hassan a Beremís. Gracias a mi eficiente intervención, podríamos, ahora, vivir tranquilos en Bagdad.
- Es interesante –respondió Beremís-. Esas líneas escritas por nuestro buen amigo Hassan me hacen recordar una curiosidad numérica relativa a los números 1, 8 y 27.
Y como viese que yo demostrara sorpresa al oír aquella observación, él concluyó:
- 1, 8 y 27 son los únicos números que son cubos perfectos e iguales, también, a la suma de los guarismos de sus cubos. Por ejemplo:
13 = 1
83 = 512
273 = 19.683
La suma de las cifras de 512 es 8.La suma de las cifras de 19.683 es 27. [125]
- Es increíble, amigo mío –exclamé-. ¡Preocupado con los cubos y cuadrados, olvidas que estabas amenazado por el puñal de un peligroso asesino!
- La Matemática, bagdalí –respondió- ocupa tanto nuestra atención que, a veces, nos aislamos de todos los peligros que nos rodean.
En seguida me contó lo siguiente:
- Cuando la ciudad de Siracusa fue tomada por asalto por las fuerzas de Marcelo, general romano, se hallaba Arquímedes absorto en el estudio de un problema, para cuya solución había trazado una figura geométrica en la arena. Un legionario romano lo encontró y le ordenó comparecer ante Marcelo. El sabio le pidió que esperase un momento, para poder concluir la demostración que estaba haciendo. El soldado insistió y lo tomó por un brazo. –“Vea donde pisa” –le dijo el geómetra-. “No me borre la figura”. Irritado por no ser inmediatamente obedecido, el sanguinario romano, con un golpe de espada, dejó sin vida al sabio más grande de todos los tiempos. Marcelo, que había dado órdenes en el sentido que se respetara la vida de Arquímedes, no ocultó el pesar que sintió al saber la muerte del genial adversario. Sobre la tumba que mandó erigir, hizo grabar una esfera inscrita en un cilindro, figura que recordaba uno de los teoremas del célebre geómetra.
Capítulo 26
En el cual vamos por segunda vez al palacio del rey. La extraña sorpresa. Los siete sabios. La devolución de un anillo. El sabio Mohadebe y la cultura religiosa. Las quince relaciones numéricas sacadas del Corán. Jesús es citado 19 veces. Un error de Beremís.
Se esperaba un gran acontecimiento. El calculista iba a ser enfrentado, en audiencia pública, a siete sabios famosos, tres de los cuales habían llegado días antes del Cairo.
¡Qué hacer! ¡Alahur Acbar! [127] Ante aquella perspectiva, procuré dar valor a Beremís, haciéndole comprender que él debía tener confianza en su capacidad, tantas veces comprobada.
El calculista me recordó un proverbio que oyera a su maestro No-Elin: “Quien no desconfía de sí no merece la confianza de los demás.”
Entramos en el palacio con grandes aprensiones y una sombra de tristeza.
La grande y rutilante Sala de Audiencias profusamente iluminada, aparecía llena de cortesanos y sheiks de renombre.
A la derecha del califa se hallaba el joven príncipe Cluzir Schá, convidado de honor, que se hacía acompañar por ocho doctores hindúes, ostentando lujosos ropajes de oro y terciopelo, y exhibiendo elegantes turbantes de Cachemira. A la izquierda del trono se hallaban los visires, los poetas, cadís, y elementos de la más alta sociedad de Bagdad. Sobre un estrado, donde veían varios cojines de seda, se hallaban los siete sabios que debían interrogar al calculista. A un gesto del califa, el sheik Nuredin Zarur tomó a Beremís de un brazo y lo condujo con toda solemnidad, hasta una especie de tribuna erigida en el centro del rico salón.
Un gigantesco esclavo negro hizo sonar por tres veces un pesado “gong” de plata. Todos los turbantes se inclinaron. Y así comenzó la singular ceremonia.
Un “imman” tomo el Libro Santo y leyó, con una cadencia invariable, separando lentamente las palabras, la oración de “Fatihat” [128].
- ¡En nombre de Alah, Clemente, Misericordioso!
¡Loado sea el Omnipotente, creador de todos los mundos!
¡La misericordia es en Dios atributo supremo!
¡Nosotros Te Adoramos, Señor, e imploramos Tu divina gracia!
¡Condúcenos por el camino verdadero! ¡Por el camino de aquellos que son iluminados y bendecidos por Tí!
Después que la última palabra del “imman” se perdió con su cortejo de ecos por las galerías del palacio, el rey caminó dos o tres pasos, se paró y dijo:
- ¡Ualá! Nuestro amigo y aliado, el príncipe Cluzir-el-din-Mouberec Schá, señor de Laore y Delhi, me pidió proporcionara a los doctores de su comitiva una oportunidad de admirar la cultura y la habilidad del geómetra persa, secretario del visir Ibraim Maluf. Hubiera sido descortés no acceder al deseo de nuestro ilustre huésped. Es por eso, que siete de los más grandes “ulemas” del Islam van a proponer sal calculista Beremís cuestiones que se relacionen con la ciencia de los números. Si él sabe responder a todas las preguntas recibirá (así lo prometió) una recompensa tal, que lo hará uno de los hombres más envidiados de Bagdad.
En ese momento vimos al poeta Iezid aproximarse al califa.
- Comendador de los Creyentes –dijo el sheik-. Tengo en mi poder un objeto que pertenece al calculista. Se trata de un anillo encontrado en mi casa por una de las esclavas del “harén”. Quiero devolvérselo al calculista antes de ser iniciada la importantísima prueba a que va a someterse. Es posible que se trate de un talismán, y no deseo privarlo del auxilio de los recursos sobrenaturales.
Permitió el monarca que el anillo fuese entregado, en ese mismo momento, al calculista
Beremís se mostró profundamente emocionado al recibir la joya. A pesar de la distancia a que me hallaba, pude notar que alguna cosa seria le ocurría en aquel momento. Al abrir la pequeña cajita, sus ojos brillantes se humedecieron. Supe después, que, conjuntamente con el anillo, la piadosa Telassim había colocado un papel en el cual Beremís leyó emocionado: “Ánimo. Confía en Dios. Rezo por ti.” ¿Estaría enterado el sheik Iezid de ese mensaje secreto?
Hízose profundo silencio. El sabio designado para comenzar el interrogatorio, se levantó. Era un anciano octogenario, de venerable figura; larga barba blanca llegábale hasta el pecho.
- ¿Quién es aquel anciano? -preguntó, en voz baja, a un espectador de delgado y bronceado rostro que se hallaba a mi lado.
- Es el célebre Mohadebe Ibagué-Abner-Raman –me respondió-. Dicen que conoce más de quince mil libros sobre el Corán. Enseña Teología y Retórica.
El sabio Mohadebe pronunciaba las palabras con un tono extraño y sorprendente, sílaba por sílaba, como si el orador pusiese empeño en medir el sonido de su voz:
- Voy a interrogarle, calculista, sobre un tema de indiscutible importancia para la cultura de un musulmán. Antes de estudiar la ciencia de un Euclides o de un Pitágoras, todo musulmán debe conoce profundamente el problema religioso, pues la vida no puede concebirse si se aparta de la Verdad y la Fe. Aquel que no se preocupa por los problemas de su existencia futura, por la salvación de su alma y que desconoce los preceptos de Dios, no merece el calificativo de sabio. Quiero, por ello, que nos digas, en este momento, y sin la menor vacilación, quince referencias numéricas, notables y exactas, sobre el Corán, el libro de Alah.
El silencio fue profundo. Se esperaba con ansiedad la respuesta de Beremís. Con una tranquilidad que asombraba, el joven calculista dijo:
- El Corán, sabio y venerable “mufti”, se compone de 114 suratas, de las cuales 70 fueron dictadas en la Meca y 44 en Medina. Se divide en 611 “aschrs” y contiene 6236 versículos, de los cuales, 7 son del primer capítulo, “Fatihat”, y 8 del último, “Los hombres”. La surata mayor es la segunda y consta de 280 versículos. El Corán contiene 46.439 palabras y 323.670 letras, cada una de las cuales encierra diez virtudes especiales. Nuestro sagrado libro, cita el nombre de 25 profetas. Issa, hijo de María [129], es citado 19 veces. Hay cinco animales cuyos nombres fueron tomados como epígrafes de cinco capítulos: la vaca, la abeja, la hormiga, la araña y el elefante. La surata 102 tiene por título “La contestación de los números”. Ese capítulo del Libro Sagrado es notable por la advertencia que, en sus 5 versículos, dirige a los que se preocupan por discusiones inútiles sobre números, que no tienen importancia alguna en el progreso espiritual del hombre. Esos son los datos sacados del Libro de Alah, para complacer nuestro pedido. Hubo, no obstante, en la respuesta que acabo de dar, un error que me apresuro a confesar. En vez de 15 referencias, cité 16.
Confirmó el sabio Mohadebe todas las referencias dadas por el calculista; hasta el número de letras le Libro de Alah, fue dicho sin el menor error.
Capítulo 27
En el cual un sabio historiador interroga a Beremís. El geómetra que no podía mirar el cielo. La Matemática en Grecia. Elogio de Eratóstenes.
Así fue como el sabio historiador se dirigió a Beremís:
- En nombre de Alah, Clemente y Misericordioso. Se equivocan los que aprecian el valor de un matemático por la mayor o menor habilidad con que efectúa las operaciones y aplica las reglas banales del cálculo. A mi manera de ver, el verdadero geómetra es el que conoce, con absoluta seguridad, el desenvolvimiento y el progreso de la Matemática a través de los siglos. Estudiar la Historia de la Matemática es rendir homenaje a los ingenios maravillosos que enaltecieran y dignificaran las antiguas civilizaciones, y que, por su labor y por su genio, pudieron revelar algunos de los profundos misterios de la Naturaleza, consiguiendo, por la ciencia, elevar y mejorar la miserable condición humana. Nos corresponde pues honrar en las páginas de la Historia a los gloriosos antepasados que trabajaran para la formación de la Matemática, y reseñar las obras que dejaran. Quiero, pues, calculista, interrogarte sobre un hecho interesante en la Historia de la Matemática: “¿Cuál fue el célebre geómetra que se suicidó de disgusto por no poder mirar al cielo?”
Beremís reflexionó unos instantes y exclamó de repente:
- Fue Eratóstenes[130], matemático oriundo de Cirenaica y educado, al principio, en Alejandría y, más tarde, en la Escuela de Atenas, donde aprendió las doctrinas de Platón.
Y completando su respuesta prosiguió:
Eratóstenes fue elegido para dirigir la gran biblioteca de la Universidad de Alejandría, cargo que ejerció hasta el fin de sus días. A más de poseer innumerables conocimientos científicos y literarios que lo distinguieron entre los mayores sabios de su tempo, fue Eratóstenes, poeta, orador, filósofo y también atleta consumado. Basta decir que mereció el excepcional título de “pentatlos”, conferido en aquel tiempo al atleta que saliese vencedor en las cinco lunas de los Juegos Olímpicos. Grecia se hallaba, en ese tiempo, en el período áureo de su desenvolvimiento científico y literario. Era la patria de los aedos, poetas que declamaban, con acompañamiento de música, en las refecciones y reuniones de reyes y jefes, los célebres poemas homéricos, largas narraciones en verso de las hazañas de los héroes, formando un conjunto de rapsodias en que las costumbres, las lenguas y las creencias se describen con admirable simplicidad de expresión, justeza de detalles y sinceridad de sentimientos. Brilló en Grecia el alma grande de Sócrates, quien, habiéndose dedicado en la mocedad a estudios de Física y Astronomía, sufrió más tarde la influencia del teísmo filosófico de Anaxágoras, creando la ley dominante de toda su filosofía: el Bien, considerado como efecto esencial de la inteligencia y de la ciencia. Combatiendo la falsa retórica y los sofismas, que enseñaban el arte de razonar y de sustentar indiferentemente todas las opiniones, Sócrates tomó la moral como base de la Filosofía, encabezando sus preceptos con el célebre aforismo: “Conócete a ti mismo”, que se leía en el frente del templo de Delfos.
No es exceso de detalles, el comentar que entre los griegos de cultura y valor, el sabio Eratóstenes era considerado como un hombre extraordinario, que tiraba la jabalina, escribía poemas, vencía a los grandes corredores y resolvía problemas de Astronomía. Eratóstenes legó a la posteridad varias obras. Presentó al rey Ptolomeo III de Egipto, una tabla de números primos hechos sobre una plancha metálica, en la cual los números compuestos eran marcados con un pequeño agujero. Diósele, por eso, el nombre de “Criba de Eratóstenes” al procedimiento que utilizara el astrónomo griego para formar su tabla de números primos. Como consecuencia de una oftalmia, que se le declarara durante un viaje a orillas del Nilo, Eratóstenes quedó ciego. Él, que cultivara la Astronomía, se hallaba impedido de mirar al cielo y admirar la belleza incomparable del firmamento en las noches estrelladas. ¡La luz eterna de “Suhhel” [131] no podría vencer jamás aquella nube negra que cubría sus ojos! Amargado por tan grande desgracia y no pudiendo resistir al disgusto que le causara la ceguera, el sabio se suicidó, dejándose morir de hambre.
- ¡Oh! –exclamó el califa-. No me precio de saber si esa respuesta es más completa que la primera.
Y poniendo su mano sobre el hombro del príncipe, añadió:
- Vamos a ver, ahora, si el tercer contendor consigue vencer a nuestro calculista.
Capítulo 28
En el cual el tercer sabio interroga a Beremís. La falsa inducción. Como se halla la raíz cuadrada de 2025. Beremís demuestra como un principio falso, puede surgir de ejemplos verdaderos.
El astrónomo Abulhasan se dirigió a Beremís. Su voz baja y cavernosa sonaba gravemente:
- Las dos respuestas que terminas de formular prueban, Beremís Samir, que posees sólida cultura. Hablas de la ciencia de Grecia con la misma facilidad con que cuentas las letras del Libro Sagrado. En el desenvolvimiento de la ciencia matemática, la parte más interesante es la que indica la forma de raciocinio que nos conduce a la verdad. Una colección de hechos está tan lejos de ser una ciencia, como un montón de piedras de ser una casa. Puedo afirmar, igualmente, que las combinaciones inteligentes de hechos inexactos, o que no hayan sido verificados, al menos en sus consecuencias, se hallan tan lejos de formar una ciencia, como un espejismo de sustituir, en el desierto, la presencia real de un oasis. La Ciencia debe observar hechos para de ellos deducir leyes; con el auxilio de éstas, prever otros hechos y mejorar las condiciones materiales de la vida. Todo esto es cierto; mas, ¿cómo deducir la Verdad? Se presenta, pues, la siguiente duda:
- ¿Es posible, en Matemática, deducir una regla falsa de una propiedad verdadera? Quiero conocer tu respuesta, ilustrada con un ejemplo simple y perfecto.
Beremís meditó largo rato y luego, saliendo de su recogimiento, respondió:
- Admitamos que un algebrista curioso desease determinar la raíz cuadrada de un número de cuatro cifras. Sabemos que la raíz cuadrada de un número es otro número que, multiplicado por sí mismo, da un producto igual, al número dado.
Vamos a suponer, sin embargo, que el calculista, al escoger los números, hiciera recaer su elección en los números: 2025, 3025, 9801.
Iniciemos la resolución del problema por el número 2025. Hechos los cálculos para ese número, el investigador hallaría que la raíz cuadrada es 45. En efecto: 45 veces 45 es igual a 2025. Ahora bien: como se puede verificar, 45 se obtiene por la suma de 20 + 25, que son parte del número 2025, descomponiéndolo por medio de un punto 20.25.
Lo mismo verificaría el algebrista para el número 3025, cuya raíz cuadrada es 55.[133] Es conveniente hacer notar que 55 es la suma de 30 + 25, partes del número 30.25.
Idéntica propiedad se verifica con respecto al tercer número, 9801, cuya raíz cuadrada es 99, esto es, 98 + 01.
Frente a esos tres caos, el desprevenido algebrista podría enunciar la siguiente regla.
“Para calcular la raíz cuadrada de un número de cuatro cifras se divide ese número por un punto, en dos grupos de dos cifras cada uno, sumándose los grupos así formados. La suma obtenida será la raíz cuadrada del número dado.”
Esa regla, visiblemente equivocada, fue deducida de tres ejemplos verdaderos. Es posible llegar a la verdad, en Matemática, por simples observaciones; no obstante son necesarias precauciones esenciales para no caer en la “falsa inducción”.
El astrónomo Abulhasan, sinceramente en cantado con la respuesta de Beremís, declaró que nunca había oído sobre la importante cuestión de la “falsa inducción matemática” explicación tan interesante y sencilla.
A continuación se paró el cuarto sabio y se preparó para formular su pregunta.
Nunca olvidaré su erguida y venerable figura, ni dejaré de recordar su mirada serena y bondadosa. Caminó hasta el extremo del estrado y así habló al sultán:
- Para que mi pregunta pueda ser bien interpretada, necesito aclararla contando una antigua leyenda persa.
- Cuéntala, ¡oh sabio elocuente! –respondió el califa-. Estamos ansiosos de oírte.
Cruzó el sabio las manos sobre el pecho y con voz firme y cadenciosa, como el andar de una caravana, contó lo siguiente:
Capítulo 29
En el cual oímos una antigua leyenda persa. Lo material y lo espiritual. Los problemas humanos y trascendentales. La famosa multiplicación. El sultán reprime con energía, la intolerancia de los sheik.
¿Qué hizo el rey Astor? Vale la pena recordar la forma como procedió el poderoso monarca.
Mandó llamar a los tres más grandes sabios de Persia, le entregó a cada uno de ellos dos denarios de plata y les dijo:
- Hay en este palacio tres salas igualmente vacías. Cada uno de vosotros deberá llenar una sala, no pudiendo emplear en esa tarea más dinero del que acabo de confiar a cada uno.
El problema rea, realmente, difícil. Cada sabio debía llenar una sala vacía gastando apenas la insignificante suma de dos denarios.
Los sabios partieron a cumplir la misión que les había encomendado el caprichoso rey Astor.
Horas después regresaron a la sala del trono.
El rey, interesado en la solución del enigma, los interrogó.
El primero dijo:
- Señor, gasté dos denarios, y la sala que me corresponde quedó completamente llena. Mi solución fue muy práctica. Compré varias bolsas de heno y con él llene la habitación desde el suelo hasta el techo.
- ¡Muy bien! –exclamó el rey-. Vuestra solución, simple y rápida, ha sido realmente muy bien concebida. Conoces, a mi modo de ver, la “parte material de la vida”, y bajo ese aspecto puedes encarar todos los problemas que un hombre debe enfrentar sobre la tierra.
A continuación, el segundo sabio habló así, después de saludar al rey:
En el desempeño de la tarea que me fuera encomendada, gasté apenas medio denario. Explicaré cómo procedí. Compré una vela y la encendí en medio de la sala vacía. Ahora, ¡oh rey!, puedes observarla. Está llena, enteramente llena de luz.
- ¡Bravo! –accedió el monarca-. Descubriste una solución brillante para el problema, la luz simboliza la parte espiritual de la vida. Vuestro espíritu, saco en conclusión, es capaz de encarar todos los problemas de la existencia desde el punto de vista espiritual.
Llegó finalmente, al tercer sabio el turno de hablar. He aquí como resolvió la singular situación:
Pensé al principio, ¡oh rey del Tiempo!, en dejar la sala entregada a mi cuidado, exactamente como se hallaba. Era fácil deducir que la sala referida, ahora cerrada, no estaba vacía, pues es evidente que estaba llena de aire y polvo. No quise, sin embargo, permanecer ocioso, mientras mis dos colegas discurrían con tanta inteligencia y habilidad. Decidí accionar yo también. Tomé, pues, un puñado de heno de la primera sala, quemé se heno con la vela que se hallaba en la otra, y, con el humo que se desprendía, llené enteramente la tercera sala. Es inútil añadir que no gasté la menor cantidad del dinero que me fue entregado.
- ¡Admirable! –exclamó el rey Astor-. Sois el más grande sabio de Persia, y tal vez del mundo. Sabéis reunir con habilidad mesurada, lo material y lo espiritual para lograr la perfección.
Terminada la narración, el sabio se volvió a Beremís, a quien dijo:
- Es mi deseo, calculista, verificar sí, a semejanza del tercer sabio de la leyenda, eres capaz de reunir lo material y lo espiritual, y llegar a resolver no sólo los problemas humanos, sino también las cuestiones trascendentales. Mi pregunta es, por lo tanto, la siguiente: “¿Cuál fue la famosa multiplicación, recordada en la Historia, multiplicación que todos los hombres cultos conocen, y en la cual figura un solo factor?”
Esa inopinada pregunta sorprendió, y con razón, a los ilustres musulmanes. Algunos no disimularon pequeños gestos de desagrado e impaciencia. Un “cadi” obeso, ricamente vestido, que se hallaba a mi lado, murmuró, irritado:
- ¡Eso no tiene sentido! ¡Es un disparate!
Beremís permaneció largo rato meditabundo.
- La única multiplicación famosa, con un solo factor, citada por los historiadores y que todos los hombres cultos conocen, es la multiplicación de los panes hecha por Jesús, hijo de María. En esa multiplicación sólo figura un factor: ¡el poder milagroso de la voluntad de Dios!
Algunos musulmanes intolerantes, se miraron espantados. Hubo murmullos. El califa exclamó con energía:
- ¡Silencio! Veneremos a Jesús, hijo de María, cuyo nombre es citado diecinueve veces en el Libro de Alah.
Y a continuación, dirigiéndose al quinto sabio, añadió plácidamente:
- Aguardamos vuestra pregunta, ¡oh sheik!
Al oír esas palabras, el quinto sabio se levantó como si fuese impulsado por un resorte. Era un hombre bajo, grueso, de blanca cabellera. En vez de turbante usaba un pequeñísimo gorro verde. Al hablar lo hacía en forma arrebatada y nerviosa.
- El valor de un sabio –comenzó con tétrica entonación- sólo puede ser medido por el poder de su imaginación. Números tomados al acaso, hechos históricos recordados con oportunidad y precisión, pueden tener momentáneo interés, mas al cabo de algún tiempo caen en el olvido. ¿Quién de nosotros se acuerda ahora del número de letras del Corán? Hay números, palabras, nombres y obras que están, por su propia naturaleza y finalidad, condenados a irremediable olvido. Voy, por lo tanto, a convencerme del valor y la capacidad del calculista persa preguntándole una cuestión que no tiene que ver con problemas que exijan memoria o habilidad de cálculo. Quiero que el matemático Beremís Samir nos cuente una leyenda en la cual aparezca indicada una división de 3 por 3, pero no efectuada, y otra de 3 por 2, indicada y efectuada sin dejar resto.
Beremís se quedó mudo, como si la inesperada pregunta del sabio lo atolondrase. Era preciso tener la suerte de recordar, en el momento, una leyenda que encerrase dos divisiones numéricas.
Después de algunos instantes de azaroso rememorar el calculista inició la siguiente narración.
Capítulo 30
En el cual Beremís narra una leyenda. El tigre sugiere la división de 3 por 3. El chacal indica la división de 3 por 2. En el cual el chacal se queda con el resto de la división. Como se calcula el cociente en la Matemática del más fuerte.
El león, el tigre y el chacal, abandonaron, cierta vez, la gruta sombría en que vivían, y salieron en peregrinación amistosa, a recorrer el mundo, en procura de alguna región rica en rebaños de tiernas ovejas.
En medio de la selva, el león, que dirigía, naturalmente, el grupo, se sentó, fatigado, sobre sus patas traseras, e irguiendo su enorme cabeza soltó un rugido tan fuerte, que hizo estremecer a los árboles más próximos.
El tigre y el chacal se miraron asustados. Aquel rugido amenazador con que el peligroso monarca, de oscura cola y garras invencibles, turbara el silencio del bosque, traducido a un lenguaje al alance de todos los animales, quería decir, lacónicamente: “-Estoy con hambre.”
- Vuestra impaciencia es perfectamente justificable (observó el chacal, dirigiéndose humildemente al león). Os aseguro, sin embargo, que conozco, en esta floresta, un atajo misterioso, del cual las fieras no tuvieron nunca noticia. Por el podríamos llegar, con facilidad, a un pequeño poblado casi en ruinas, donde la caza es abundante, fácil, al alcance de las garras, y exenta de cualquier peligro.
- Vamos, chacal –dijo de pronto el león-; quiero conocer y admirar ese adorable lugar.
Al caer de la tarde, guiados por el chacal, llegaron los viajeros a lo alto de un monte no muy elevado, desde donde se divisaba una pequeña y verde planicie.
En medio del valle se hallaban descuidados, ajenos a los peligros que los amenazaban, tres pacíficos animales: una oveja, un cerdo y un conejo.
Al avistar la fácil presa, el león sacudió la abundante melena en un movimiento de incontenida satisfacción. Y con los ojos brillantes de gula, se volvió hacia el tigre y gruñó, con tono posiblemente amistoso:
- ¡Oh, tigre admirable! Veo allí tres hermosos y sabrosos manjares; una oveja, un cerdo y un conejo. Tú, que eres listo y experto, debes saber dividir con talento tres entre tres. Haz, pues, con justicia y equidad, esa operación fraternal: dividir tres entre tres cazadores.
Lisonjeado con semejante proposición, el vanidoso tigre, después de expresar con visos de falsa modestia su incompetencia y su poco valor, respondió así:
- La división que generosamente acabáis de proponer -¡oh rey!- es muy simple y se puede hacer con bastante facilidad. La oveja, que es el mayor de los tres bocados, y el más sabroso, y, sin duda, capaz de saciar el hambre de un grupo de leones del desierto, os toca por derecho. Aquel cerdo flaco, sucio y maloliente, que no vale una pierna de la hermosa oveja, será para mí, que soy modesto y con bien poco me conformo. Y, finalmente, aquel minúsculo y despreciable conejo, de reducidas carnes, indigno del paladar refinado de un rey, corresponderá a nuestro compañero el chacal, como recompensa por la valiosa indicación que hace poco nos proporcionó.
- ¡Estúpido, egoísta! –rugió, enfurecido, el león, lleno de indescriptible furia-. ¿Quién te enseñó a hacer divisiones de esa manera? ¿Dónde viste una división de tres por tres, hecha de ese modo?
Y, levantando su pesada pata, descargó sobre la cabeza del desprevenido tigre tan violento golpe, que lo tiró muerto a algunos pasos de distancia.
En seguida se volvió al chacal, que asistiera aterrado a aquel trágico final de la división de tres por tres y así le habló:
- Mi querido chacal. Siempre tuve de tu inteligencia el más alto concepto. Sé que eres el más ingenioso y brillante de los animales de la floresta, y no conozco otro que pueda aventajarte en la habilidad con que sabes resolver los más intrincados problemas. Te encomiendo, pues, el hacer esa división simple y banal, que el estúpido tigre (como ya acabaste de ver) no supo efectuar satisfactoriamente. ¿Estás viendo, amigo chacal, aquellos apetitosos animales: la oveja, el cerdo y el conejo? Pues bien: dividirás las tres piezas entre nosotros dos. ¡Nada más sencillo que dividir tres por dos! Haz los cálculos, pues deseo saber qué cociente exacto me corresponde.
- No soy más que un humilde y rudo siervo de Vuestra Majestad –dijo el chacal, en tono humildísimo de respeto-. Debo, pues, obedecer ciegamente la orden que acabo de recibir. Voy a dividir, como si fuera un sabio geómetra, aquellas tres piezas entre nosotros dos. La división matemáticamente exacta es la siguiente. La admirable oveja, manjar digna de un soberano, es para vuestros reales caninos, pues es indiscutible que sois el rey de los animales; el bello cerdo, del cual oigo los armónicos gruñidos, debe ser también para vuestro real paladar, pues, según dicen los entendidos, la carne de puerco da más fuerza y energía a los leones; y el inquieto conejo, con sus largas orejas, debe ser saboreado por vos, como sobremesa, ya que a los reyes, por ley tradicional entre los pueblos, les pertenecen, de los opíparos banquetes, los manjares más finos y delicados.
- ¡Chacal incomparable! –exclamó el león, encantado con el reparto que acababa de oír-. ¡Qué agradables y sabias son tus palabras! ¿Quién te enseñó ese artificio maravilloso para dividir con tanta perfección y acierto, tres por dos?
- Es zarpazo con que vuestra justicia castigó, hace un instante, al tigre arrogante y ambicioso, me enseñó a dividir con certeza tres por dos cuando de esos dos uno es el león y otro el chacal. En las matemáticas del más fuerte, pienso que el cociente es siempre exacto, y al más débil, después de la división, ni el resto le debe tocar.
Y, desde ese día en adelante, haciendo siempre divisiones de esa manera, inspiradas en el más torpe servilismo, vivió el astuto chacal su vida de vil adulador, regalándose con los desechos que dejaba el león.
- He aquí, elocuente “ulema” -concluyó Beremís-, una leyenda en la cual aparecen dos divisiones. La división de 3 por 3 fue apenas indicada, y la otra, de 3 por 2, efectuada sin dejar “resto”.
Quedó encantado el sultán al oír la admirable fábula contada por el calculista.
Ordenó que la “División de tres por tres” fuese conservada en los archivos del califato, pues la narración de Beremís, por sus elevadas finalidades morales merecía ser escrita con letras de oro en las alas transparentes de una mariposa blanca del Cáucaso.
Y, a continuación, tomó la palabra el sexto “ulema”.
El sexto sabio era un cordobés. Había vivido quince años en España y de allá había huido por haber caído en desgracia con un príncipe musulmán. Hombre de media edad, de cara redonda y fisonomía franca y sonriente, decían de él sus admiradores que era muy hábil para escribir versos humorísticos o sátiras contra los tiranos.
¡Emir del Mundo! –comenzó el cordobés, dirigiéndose al sultán-. Acabo de oír con verdadero placer esa admirable fábula intitulada “La división del persa”. Encierra ella, a mi modo de ver, grandes enseñanzas y profundas verdades. Verdades claras como la luz del sol en la hora de “edduhhr” [134]. Me veo obligado a confesar que los preceptos matemáticos toman forma viva cuando son presentados bajo la forma de fábulas o de historias. Conozco una leyenda que no contiene divisiones, cuadrados o fracciones, mas encierra un problema de Lógica, posible de resolver con un razonamiento puramente matemático. Contada la historia, veremos cómo podrá el eximio calculista resolver el problema en ella contenido.
Y el sabio cordobés contó lo siguiente:
Capítulo 31
En el cual el sabio cordobés cuenta una leyenda. Los tres novios de Dahizé. El problema de los cinco discos. Como Beremís reprodujo el raciocinio de un novio inteligente.
- ¡Qué exageración!, diréis.
No admito la exageración, hermano de los árabes. La exageración es una forma disfrazada de mentir.
Pasemos, sin embargo, al caso que nos interesa.
Cuando Dahizé cumplió 18 años de edad, fue pedida en matrimonio por tres príncipes cuyos nombres perpetuó la tradición: Aradín, Benefir y Camozan.
El rey Bassin quedó indeciso. ¿Cómo elegir entre los tres ricos pretendientes, aquel que sería el novio de su hija? Hecha la elección, la consecuencia inevitable sería que él, el rey, ganaría un yerno, pero, en cambio, se haría de dos rencorosos enemigos. Mal negocio para un monarca sensato y prudente, que deseaba vivir en paz con su pueblo y sus vecinos.
Consultada la princesa Dahizé, declaró que se casaría con el más inteligente de sus admiradores.
La decisión de la joven fue recibida con alegría por el rey Cassim. El caso, que parecía tan complicado, tenía, sin embargo, una solución muy simple. El soberano árabe mandó llamar a cinco de los más grandes sabios de la Corte y les dijo que sometiesen a los príncipes a un riguroso examen.
Terminadas las pruebas, los sabios presentaron al rey un minucioso informe. Los tres príncipes eran inteligentísimos. Conocían profundamente la Matemática, Literatura, Astronomía y Física; resolvían complicados problemas de ajedrez, cuestiones sutilísimas de Geometría, enigmas arrevesados y oscuras charadas.
- No hallamos medio alguno –concluyeron los sabios- que nos permitiese llegar a un resultado definitivo a favor de uno o de otro.
Frente a ese lamentable fracaso de la ciencia, resolvió el rey consultar a un derviche que tenía fama de conocer la magia y los secretos del ocultismo.
El sabio derviche dijo al rey:
- Sólo conozco un medio que permitirá determinar cuál es el más inteligente de los tres. Es la prueba de los cinco discos.
- Hagamos, pues, esa prueba –accedió el rey.
Los príncipes fueron llevados al palacio. El derviche, mostrándoles cinco discos de cartón, les dijo:
- He aquí cinco discos, dos de los cuales son negros y tres blancos. Observen que son del mismo tamaño y del mismo peso, y que solo difieren en el color.
A continuación un paje vendó cuidadosamente los ojos de los tres príncipes, impidiéndoles así ver la menor luz.
El viejo derviche tomó entonces al azar tres de los cinco discos y los prendió a la espada de los tres príncipes.
Dijo entonces el derviche:
- Cada uno de vosotros lleva a cuestas un disco, cuyo color ignora. Seréis interrogados uno a uno. Aquel que descubra el color del disco que le cupo en suerte, será declarado vencedor y se casará con la linda Dahizé. El primero que sea interrogado podrá ver los discos de los otros dos concursantes; al segundo le será permitido ver el disco del último. Este tendrá que formular la respuesta sin ver disco alguno. Aquel que formule la respuesta exacta, para probar que no fue favorecido por el azar, tendrá que justificarla por medio de un razonamiento riguroso, metódico y simple. ¿Cuál de vosotros desea ser el primero?
Respondió prontamente el príncipe Camozan:
- Quiero ser el primero en responder.
El paje retiro la venda que cubría los ojos del príncipe Camozan, y este pudo ver el color de los discos que se hallaban sobre las espaldas de sus rivales.
Interrogado, en secreto, por el derviche, no acertó en su respuesta. Fue declarado vencido, y debió retirarse de la sala.
El rey anunció en voz alta, a fin de prevenir a los otros dos:
- El joven Camozan acaba de fracasar.
- Quiero ser el segundo –dijo el príncipe Benefir.
Desvendados los ojos, el príncipe vio la espalda de su competidor y vio el color de su disco. Aproximóse al derviche y le dijo en secreto su respuesta:
El derviche sacudió negativamente la cabeza. El segundo príncipe había errado, y fue, por consiguiente, invitado a dejar el salón.
Quedaba aún el tercer concursante, el príncipe Aradín.
Este, luego que el rey anunció la derrota del segundo pretendiente, se aproximó al trono, con los ojos vendados, y dijo en voz alta el color de su disco.
El sabio cordobés, dirigiéndose al calculista, le preguntó:
- Deseo saber cuál fue la respuesta del príncipe Aradín y cuál el razonamiento hecho por el príncipe, que lo llevó a resolver con seguridad el problema de los cinco discos.
Beremís, con grave seriedad y sin intimidarse, habló así:
- El príncipe Aradín, el héroe de la curiosa leyenda que acabamos de oír, afirmó al rey Cassim: “Mi disco es blanco”. Y para llegar a esa conclusión hizo, con seguridad, el siguiente razonamiento:
I | II |
Negro (Benefir) | Blanco (Benefir) |
Negro (Yo) | Negro (Yo) |
III | IV |
Blanco (Yo) | Blanco (Yo) |
Negro (Benefir) | Blanco (Benefir) |
En esas diversas hipótesis no fue incluido, por no interesar al razonamiento, el color del disco del príncipe Camozan, primer concursante interrogado.
I, hipótesis.- Negro (Benefir); Negro (Yo).
Diría el príncipe Aradin:
“Admitida la primera hipótesis, esto es, si mi disco fuera negro y el de Benefir negro, el primer concursante no habría errado. En efecto: viendo dos discos negros, sabría (con absoluta certeza) que su disco era blanco, y habría respondido acertadamente.”
Ahora bien: si el primero se equivocó fue porque tuvo dudas, y, ello sólo sería posible si él hubiera visto un disco negro y otro blanco, o dos blancos. Es evidente que la hipótesis I no es aceptable y debe ser, por consiguiente, desechada.
Quedan, por lo tanto, las hipótesis II, III y IV.
II, hipótesis. Negro (Yo); Blanco (Benefir).
Diría en este caso el príncipe Aradín:
“Admitamos que la hipótesis II fuese verdadera; esto es, vamos a suponer que el disco (A) fuese negro, y el disco (B), de Benefir, blanco. El príncipe Benefir, que es muy inteligente, sabiendo en virtud del razonamiento (como consecuencia del error del primero), que nuestros discos no podían ser negros (como ya probé), concluiría diciendo que el de él era blanco, y habría acertado. Si Benefir erró, fue porque tuvo dudas, y esa duda solo podría surgir del hecho de haber visto en mis espaldas un disco blanco. ”
“Desechada la hipótesis II, como acabo de probar, sólo quedan las III y IV. En cualquiera de las dos hipótesis, mi disco es blanco.”
- Es ese, ¡oh sabio! –concluyó Beremís- el razonamiento que habría hecho el príncipe Aradín para descubrir, con absoluta seguridad, el color de su disco.
Capítulo 32
En el cual Banabixacar interroga a Beremís. Alí Babá y los cuarenta ladrones. ¡Cuarenta! ¿Por qué? Cuál es el significado simbólico de ese número. El problema de la piedra de 40 “artales”.
El séptimo y último sabio que debía interrogara Beremís, era una de las figuras más extraordinarias del Islam. Era geómetra y astrónomo, y se llamaba Mohildin Ihaia Banabixacar. Su nombre estaba escrito en cinco mezquitas y sus libros eran leídos hasta por los “roumis” [135]. Era imposible encontrar bajo el cielo del Islam, inteligencia más poderosa y culta, más sólida y vasta.
El erudito Banabixacar, con su manera clara e impecable, habló así:
- Entre las leyendas más famosas citan los narradores la admirable historia intitulada “Alí Babá y los Cuarenta Ladrones”. ¿Ese número “cuarenta” habría sido elegido al acaso, o fue elegido en virtud de principio o ley exclusivamente matemática? ¿Qué relación habrá entre el número cuarenta y los “ladrones”?
La cuestión propuesta era dificilísima y delicada. La respuesta de Beremís, sin embargo, no se hizo esperar. El calculista persa habló de la siguiente manera:
- Los ladrones que figuran en la aventura del leñador Alí Babá, son cuarenta. Desde el punto de vista matemático, presenta este número una particularidad muy curiosa, que justifica, plenamente, la preferencia dada por los narradores antiguos. ¡Cuarenta! ¿Qué hacían los ladrones para juntar riquezas y con ellas llenar la caverna? Ellos robaban, es decir, “ sustraían”. Cada robo correspondía a una sustracción. Una vez cometido el robo, los ladrones de la cuadrilla juntaban los objetos robados; tal operación equivale a una suma, o sea, a una adición. ¿Qué hacían pues los ladrones de la leyenda? Sumaban y sustraían. Pues bien: el número cuarenta es el mayor número que, descompuesto en cuatro partes desiguales, permite formar con esas partes, por medio de sumas y sustracciones, todos los números enteros desde 1 hasta 40. Esas cuatro partes, que se presentan en progresión geométrica (siendo la razón igual a 3), son: 1, 3, 9, 27
Así:
1 | = | 1 | 21 | = | 27 – 9 + 3 | |
2 | = | 3 – 1 | 22 | = | 27 – 9 + 3 + 1 | |
3 | = | 3 | 23 | = | 27 – 3 – 1 | |
4 | = | 3 + 1 | 24 | = | 27 – 3 | |
5 | = | 9 – 3 – 1 | 25 | = | 27 – 3 + 1 | |
6 | = | 9 – 3 | 26 | = | 27 – 1 | |
7 | = | 9 – 3 + 1 | 27 | = | 27 | |
8 | = | 9 – 1 | 28 | = | 27 + 1 | |
9 | = | 9 | 29 | = | 27 + 3 – 1 | |
10 | = | 9 + 1 | 30 | = | 27 + 3 | |
11 | = | 9 + 3 – 1 | 31 | = | 27 + 3 + 1 | |
12 | = | 9 + 3 | 32 | = | 27 + 9 – 3 – 1 | |
13 | = | 9 + 3 + 1 | 33 | = | 27 + 9 – 3 | |
14 | = | 27 – 9 – 3 – 1 | 34 | = | 27 + 9 – 3 + 1 | |
15 | = | 27 – 9 – 3 | 35 | = | 27 + 9 – 1 | |
16 | = | 27 – 9 – 3 + 1 | 36 | = | 27 + 9 | |
17 | = | 27 – 9 – 1 | 37 | = | 27 + 9 + 1 | |
18 | = | 27 – 9 | 38 | = | 27 + 9 + 3 – 1 | |
19 | = | 27 – 9 + 1 | 39 | = | 27 + 9 + 3 | |
20 | = | 27 – 9 + 3 – 1 | 40 | = | 27 + 9 + 3 + 1 |
Eso demuestra que los números, desde 1 hasta 40, pueden ser formados con los cuatro elementos 1, 3, 9 y 27 en que fue descompuesto el número 40.
En las cuarenta relaciones que acabo de formar, podemos observar las siguientes particularidades:
I) La primera comienza por 1; las tres siguientes por 3; las nueve siguientes por 9; las 27 siguientes por 27;
II) Cada uno de los cuatro elementos (1, 3, 9 y 27) figura 27 veces en las cuarenta diferentes relaciones.
Existe otro problema ya estudiado por los matemáticos del tiempo de Al Carisma, y cuya solución se basa en esa misma propiedad del número 40.
Ese problema es el siguiente:
Un mercader tenía una piedra que pesaba 40 “artales”. Cierta vez esa piedra se cayó y se partió en cuatro pedazos, causando gran contrariedad al mercader. Un calculista, que se hallaba presente, pasó los cuatro pedazos y dijo al mercader: “Es una división conveniente. Con esos cuatro pedazos podrás hacer cualquier pesaje desde 1 hasta 40.”
Se pregunta: ¿Cuánto pesaban los 4 fragmentos de piedra?
La solución es dada precisamente por los números 1, 3, 9 y 27.
Con esos cuatro pesos se puede hacer cualquier pesaje (en unidades enteras) desde 1 hasta 40.
El peso de 14 “artales”, por ejemplo, sería obtenido colocando el peso 27 en uno de los platos de la balanza, y los otros tres fragmentos menores en el otro plato. La diferencia de peso es 14 “artales”.
Las cuatro partes en que fue descompuesto el número 40, son, como ya dije, potencias de 3. Este número aparece (y la circunstancia es digna de hacerse notar) en casi todos los episodios de la leyenda de Alí Babá.
Cuando el pobre leñador descubrió la gruta de los ladrones, conducía tres burros cargados de leña; con ayuda de esos tres burritos trajo a su casa u tesoro fabuloso. Todavía más: tres ladrones de la cuadrilla fueron muertos por el jefe, al haber sido engañados por Luz Nocturna, que era la esclava predilecta y preferida de Alí Babá.
El envidioso Cassim, hermano de Alí Babá, sorprendido en el interior de la gruta, fue muerto por los ladrones y su cuerpo dividido en 6 pedazos. El número 6 es el doble de 3, cuyas primeras potencias suman 40. (3 0 + 31 + 32 + 33 = 40.)
Hay también con respecto a la frase mágica, “Ábrete, sésamo”, que habría la gruta encantada, relaciones numéricas dignas de observar.
Otro problema famoso en el cual aparece el número 40, es el siguiente:
“El historiador Josefo, gobernador de Galilea, que resistió heroicamente las legiones de Vespasiano, siendo vencido al final, se refugió en una caverna con cuarenta patriotas judíos. Sitiados por los romanos, prefirieron matarse todos antes de entregarse a los enemigos. Formando rueda, contaban 1, 2 y 3, y cada uno de los que le tocaba el número 3 era muerto. ¿En qué lugar correspondía estar a Josefo para escapara a esta horrible matanza?”
La solución de este problema puede obtenerse fácilmente con ayuda de un esquema práctico: basta escribir en círculo 41 números y, comenzando a contar por el primero, ir tachando con un trazo cada tres lugares.
Después de terminar toda la rueda, continuar del mismo modo, pero sin tomar en cuenta los números ya tachados, porque estos pasan a ser considerados soldados muertos. Terminado el trabajo, se ve que solo dos judíos se salvaron de aquella masacre: fueron los que se encontraban en los lugares 16 y 31. Uno de esos lugares privilegiados lo escogió para sí el gobernador Josefo, el cual en vez de matar al compañero y suicidarse después, prefirió entregarse con todas las garantías a Vespasiano.
El número 40 aparece entre las tradiciones más notables de los judíos y cristianos[136].
Creo, sin embargo, haber explicado suficientemente la significación simbólica del número cuarenta en una de las leyendas más famosas de nuestro inmenso tesoro literario.
Capítulo 33
En el cual Beremís habla de los problemas imposibles. El doble del cubo. La trisección del ángulo. La cuadratura del círculo. El número 22 y el círculo.
El gran astrónomo Benabixacar, que se hallaba a la derecha, después de aspirar largamente el perfume de un frasco que tenía en la mano, se dirigió, respetuoso, al califa en los siguientes términos:
- Me veo forzado a confesar, rey del Tiempo, que al formular el problema de los cuarenta ladrones de Alí Babá, no imaginaba que el calculista persa fuese capaz de resolverlo de manera tan brillante y completa. Fueron muchos los investigadores que incluyeron tal problema entre los que debían permanecer sin solución, burlando los recursos de la Matemática. La solución formulada por Beremís Samir es digna de figurar en las páginas de oro entre los versos de “Lamiat el-adjem”. [137]
El príncipe Cluzir Schá dijo, entonces al sultán:
- Ese sabio anciano acaba de referirse a los “problemas sin solución” de la Matemática. Sería interesante que el calculista, que ya ha aclarado tantas cuestiones difíciles, nos dijera algo sobre los problemas sin solución.
- Es magnífico lo que propones –interrumpió el sultán.
Y, dirigiéndose al calculista, le dijo:
- ¿Cuáles son los problemas famosos que los matemáticos consideran sin solución?
- En el campo de la Matemática, se presentan, ¡oh Emir de los Creyentes!, infinidad de problemas para los cuales no se ha encontrado una solución satisfactoria. Entre los que se han hecho célebres, justo es citar los siguientes:
- Problema de la duplicación del cubo.
- Problema de la trisección de un ángulo.
- Problema de la cuadratura del círculo .
Veamos en qué consisten esos problemas y cuáles fueron los intentos hechos por los matemáticos en el sentido de resolverlos.
- El problema de la duplicación del cubo, conocido en la antigüedad bajo la denominación de problema de Delos o problema deliano, se explica por medio de una leyenda que no deja de ser interesante:
Una terrible epidemia diezmaba a los habitantes de la ciudad de Atenas. Convencidos que el flagelo era castigo de los dioses, los atenienses fueron a consultar el oráculo de Delos sobre el medio que podrían valerse para acabar con el mal. Dijo el oráculo:
“ En el templo de Apolo existe un altar de forma cúbica. La epidemia cesará el día en que ese altar sea sustituido por otro exactamente igual al doble.”
Hallaron los atenienses por demás simple la condición impuesta por el oráculo y lo sustituyeron por otro altar de la misma forma y cuya arista era dos veces mayor.
La división de la circunferencia en ocho partes iguales fue un problema resuelto por los matemáticos, algunos milenios antes de Cristo. En la figura que ilustra esta página, la circunferencia de la rueda del carro egipcio está dividida en ocho partes iguales
Seguros que habían cumplido la indicación revelada por el oráculo, esperaban que la epidemia terminara. Se engañaron. La peste se volvió más mortífera. Consultaron otra vez al oráculo y éste explicó: “El nuevo altar no es el doble del primero, sino ocho veces mayor.” E insistió: “Es necesario duplicar el cubo.”Frente a esa dificultad, los atenienses apelaron a los conocimientos de los geómetras. Para ser agradable a los dioses era necesario saber Geometría, pues la Geometría es la ciencia divina.
Hipócrates[138] fue el primer geómetra que estudió el problema, consiguiendo, hasta cierto punto, aclarar la cuestión. Asquitas presentó una solución muy ingeniosa, cuya demostración geométrica y cinemática, sugerida por el gran filósofo Platón, fue analizada más tarde por Eudoxio.
Mecmeno, notable geómetra, de quien el conquistador Alejandro fue el discípulo, tratando de solucionar el problema deliano, descubrió las llamadas secciones cónicas: esto es, probó que las curvas llamadas elipse, parábola e hipérbola pueden obtenerse mediante secciones planas de un cono.
En la figura que precede vemos un carro egipcio antiguo, con una rueda en la que la circunferencia está dividida en 12 partes iguales.
Más tarde Nicomedes se dedicó también sin resultado al problema de Delos, procurando resolverlo con el auxilio de una construcción basada en una curva llamada concoide.Alah se compadezca de esos geómetras que tanto contribuyeron con sus estudios, al desenvolvimiento de la gran ciencia de Euclides.
Veamos, a continuación, en qué consiste el problema de la trisección de un ángulo.
Dado un ángulo cualquiera, dividirlo en tres ángulos iguales empleando únicamente la regla y el compás.
Un griego, llamado Hipias, se hizo célebre en la Historia de la Matemática, por el hecho de haberse ocupado del problema de la trisección del ángulo.
Hipias imaginó una curva denominada más tarde cuadratriz, con el auxilio de la cual era posible resolver el problema de la trisección del ángulo.
La cuadratriz es notable porque es la primera curva definida por vía cinemática.[139]
El filósofo Platón no aceptó la solución dada al problema por Hipias, haciendo ver que la cuestión geométrica solo podía ser resuelta con el empleo exclusivo de la regla y el compás.
Si no fuese por la condición impuesta, la curva denominada concoide de Nicomedes, aplicada al problema de la duplicación del cubo, podría ser empleada, igualmente, en el caso de la trisección del ángulo.
En la figura que precede, la cual representa a uno de los antiguos reyes, aparece una circunferencia dividida en 6 partes iguales.
De todas las cuestiones geométricas famosas, el problema de la cuadratura del círculo es uno de los que ha despertado mayor interés entre los hombres que cultivaran la Matemática.El problema de la cuadratura del círculo consiste en una construcción rigurosa, con la regla y el compás, esto es, por un número limitado de rectas y circunferencias, de un cuadrado de área igual a la de un círculo dado cualquiera.[140]
Durante más de mil trescientos años investigaron los matemáticos ese famoso problema, tratando en vano de descubrirle una solución; y el fracaso de tantos esfuerzos –traducido por la falta de éxito de todas las tentativas- llevó, al geómetra a incluir el problema de la cuadratura del círculo entre los problemas imposibles.
Así como el alquimista, obsesionado por la obsesión de descubrir la piedra filosofal, aportaba a la Química nuevos e impactantes descubrimientos, también el matemático, investigando sobre la cuadratura del círculo, trabajaba para el progreso de la ciencia.
Nos cuenta Plutarco, historiador ateniense, que el primero que se interesó por el problema de la cuadratura del círculo fue el filósofo jónico Anaxágoras, del que fue discípulo Pericles. El cultivo de la ciencia fue para Anaxágoras fuente de serios sinsabores. Por haber afirmado que el Sol excedía en magnitud a la península europea, e intentando explicar diversos fenómenos que los griegos atribuían a los dioses caprichosos del paganismo, fue condenado a prisión, y en el silencio del presidio escribió un trabajo sobre la cuadratura del círculo.
Hipócrates –once siglos antes de Mahoma- llegó a descubrir las primeras cuadraturas de superficies limitadas por curvas, cuando su objetivo único era llegar a la cuadratura del círculo.
El geómetra Dinastrato, hermano de Menecme y discípulo de Platón, reconoció que con el auxilio de una curva (cuyo descubrimiento se atribuye a Hipias) era posible resolver el problema de la cuadratura del círculo. De ahí la denominación de cuadratriz dada a la curva descubierta por el sofista griego.
El problema de la cuadratura del círculo es imposible; no menos imposible es la división euclidiana de la circunferencia en un número cualquiera de partes iguales, a causa de la relación entre la circunferencia y el diámetro[141]. Esa relación debe ser aproximadamente igual a 22/7, como leemos en el Capítulo VIII del libro de Masudi, en el cual ese autor, repitiendo los cálculos del astrónomo Hussein, afirma que la circunferencia de la Tierra multiplicada por 7 y dividida por 22, da como resultado el diámetro de la Tierra.
- ¡Príncipe de los Creyentes! Todos los fieles saben que Alah (¡exaltado sea el Altísimo!) en el Corán dice: “Los verdaderos sabios temen el nombre de Dios y adoran al Creador”. Mahoma, en cierta ocasión, afirmó con su inspirada palabra: “Procurad la instrucción. Cultivar el estudio es acción altamente meritoria a los ojos de Dios. Propagar la ciencia es una guerra santa.” La instrucción permite al hombre distinguir lo que es lícito de lo que es ilícito. En las horas solitarias encontramos en ella la más fiel compañera; en los momentos de infortunio, consejera veraz; en los tiempos felices, inestimable auxiliar. “En el día del juicio, dijo aún Mahoma (¡con Él en la oración y en la paz!), la tinta gastada por los sabios y la sangre derramada por los mártires serán pesadas en la misma balanza. Un día consagrado a las investigaciones científicas tiene más valor, a los ojos de Dios, que cien expediciones guerreras.” A la luz de esas enseñanzas eternas debemos, pues, exaltar a los que se dedican al estudio de la Ciencia, y especialmente a los sabios que cultivan la Matemática, honra del espíritu humano.
Gloria, pues, a Alah, Creador del Cielo y de la Tierra, señor de los mundos visibles e invisibles.
Capítulo 34
El califa Al-Motacen ofrece oro y palacios al calculista. Beremís los rechaza. Un pedido de casamiento. El problema de los ojos negros y azules. Como determinó Beremís, por el cálculo, el color de los ojos de cinco esclavas .
Por las respuestas dadas a todas las preguntas, calculista has hecho méritos para recibir el premio que te prometí. Dejo, por tanto, a tu lección ¿Quieres recibir veinte mil denarios de oro, o prefieres poseer un palacio en Bagdad? ¿Deseas el gobierno de una provincia, o ambicionas el cargo de visir de mi Corte?
Rey generoso –respondió Beremís, profundamente emocionado-. No ambiciono riquezas, títulos, homenajes o regalos, porque sabido es que los bienes materiales nada valen; la fama que pueda surgir de los cargos importantes no me interesa, pues mi espíritu no sueña con la gloria efímera del mundo. Si es vuestro deseo hacerme, como dijiste, envidiado por todos los musulmanes, mi pedido es el siguiente: Deseo casarme con la joven Telassim, hija del sheik Iezid Abul-Hamid.
El inesperado pedido formulado por el calculista causó indecible asombro. Me di cuenta, por los rápidos comentarios que pude oír, que todos los musulmanes que allí se hallaban no tenían la menor duda sobre el estado de demencia de Beremís.
- ¡Ese calculista es un loco, decían. Desprecia la riqueza y rechaza la gloria para casarse con una joven que nunca vio!
Cuando el califa Al-Motacen oyó el pedido de Beremís, le dijo:
- No me opondré, calculista, a tu casamiento con la hermosa Telassim. Es verdad, que esa joven ya estaba prometida a uno de los más ricos sheiks de la Corte; pero, por una vez, sin embargo, ya que ella desea cambiar el rumbo de su vida -¡mactub!-, ¡sea hecha la voluntad de Alah!
- No obstante, impongo –prosiguió enérgico el soberano- una condición. Tendrás, eximio matemático, que resolver, delante de todos los nobles que aquí se hallan, un curioso problema inventado por un derviche del Cairo. Si resuelves ese problema, te casarás con Telassim; en caso contrario, tendrás que desistir, para siempre, de esa fantasía loca de beduino que bebió “hachís”. ¿Te conviene?
- ¡Emir de los Creyentes! –respondió Beremís con tranquilidad y firmeza-. Deseo conocer los datos del aludido problema, a fin de poder solucionarlo con los prodigiosos recursos del Cálculo y del Análisis.
El poderoso califa dijo entonces:
- El problema, en su expresión más simple, es el siguiente: Tengo cinco hermosas esclavas, que compré hace pocos meses a un príncipe mongol. De esas cinco encantadoras jóvenes, dos tienen los ojos negros y las cinco restantes azules. Las dos esclavas de ojos negros “ dicen siempre la verdad”; las esclavas de ojos azules, por lo contrario, son mentirosas, esto es, “no dicen nunca la verdad”. Dentro de algunos minutos, esas cinco jóvenes serán traídas a la sala; todas tendrán el rostro cubierto por un espeso velo oscuro. El “Jaique” que las envuelve, hace imposible distinguir en cualquiera de ellas, el menor rasgo fisonómico. Tendrás que descubrir e indicar, sin el menor error, cuales son las jovencitas de ojos negros y cuales las de ojos azules. Te será permitido interrogar a tres de las cinco esclavas, no pudiendo hacer más de una pregunta a cada una. Con la ayuda de las tres respuestas obtenidas, el problema deberá ser resuelto, justificando la solución con un razonamiento matemático. Además, las preguntas deben ser de tal naturaleza, que sólo puedan ser respondidas con exactitud por las esclavas.
Momentos después, bajo la mirada curiosa de los circunstantes, aparecían en el salón de audiencias las cinco esclavas de Al-Motacén. Cubiertas con largos velos negros desde la cabeza hasta los pies, parecían verdaderos fantasmas del desierto.
Beremís sintió que llegaba el momento decisivo de su carrera. El problema formulado por el califa de Bagdad, a más de ser difícil y original, podría encerrar dudas y escollos imprevisibles.
Al calculista le era permitido interrogar a tres de las cinco jóvenes. ¿Cómo descubrir, por las respuestas, el color de los ojos de todas ellas? ¿A cuáles de las cinco debería interrogar? ¿Cómo eliminar las dudas que surgirían del interrogatorio?
Había una indicación valiosa: las de ojos negros decían siempre la verdad; las otras tres (de ojos azules) mentían siempre.
¿Bastaría eso?
Vamos a suponer que el calculista interrogase a una de ellas. La pregunta debía ser de tal naturaleza, que solo la esclava pudiera responder. Obtenida la respuesta, continuaría la duda. ¿La interrogada habría dicho verdad? ¿Habría mentido? ¿Cómo llegar al resultado, si no conocía él la respuesta exacta?
El caso era, realmente, muy grave.
Las cinco embozadas se colocaron en fila en el centro del suntuoso salón. Se hizo un gran silencio. Los nobles, musulmanes, sheiks y visires, seguían con vivo interés las alternativas de aquel nuevo y singular capricho del rey.
El calculista se aproximó a la primera esclava (que se hallaba en el extremo de la fila, a la derecha) y le preguntó con voz firme y reposada:
- ¿De qué color son tus ojos?
¡Por Alah! A interpelada respondió en un dialecto chino, totalmente desconocido para los musulmanes presentes. Beremís protestó. No comprendió una sola palabra de la respuesta dada.
El califa ordenó que las respuestas fueran dadas en árabe, y de una manera clara y sencilla.
Aquel inesperado fracaso, vino a agravar la situación del calculista. Quedábanle apenas dos preguntas, pues la primera era considerada enteramente perdida para él.
Beremís, a quien el hecho no había logrado desalentar, se volvió a la segunda esclava y le preguntó:
- ¿Cuál fue la respuesta que tu compañera acaba de dar?
- Las palabras de ella fueron: “Mis ojos son azules”.
Esa respuesta nada aclaraba. ¿La segunda esclava habría dicho la verdad o estaría mintiendo? ¿Y la primera? ¿Quién podía confiar en sus palabras?
La tercera esclava (que se hallaba en el centro de la fila) fue interrogada a continuación, por Beremís, en la siguiente forma:
- ¿De que color son los ojos de esas dos jóvenes que acabo se interrogar?
A esa pregunta –que era la última que `podía formular –la esclava respondió:
- La primera tiene los ojos negros y la segunda azules.
¿Sería verdad? ¿Habría mentido?
Lo cierto es que Beremís, después de meditar algunos minutos, se aproximó tranquilo al trono y dijo:
- ¡Comendador de los Creyentes! ¡Sombra de Alah sobre la Tierra! El problema propuesto está resuelto por completo y su solución puede ser anunciada con exactitud matemática. La primera esclava (la de la derecha) tiene los ojos negros, la segunda azules, la tercera negros, y las dos últimas tienen los ojos azules.
Levantados los velos y retirados los pesados “haics”, las jóvenes mostraron sonrientes los rostros descubiertos. Se oyó un ¡ah! De asombro en el gran salón. El inteligente Beremís había dicho, con admirable precisión, el color de los ojos de todas ellas.
- ¡Por las barbas de Mahoma! –exclamó el rey- ¡Ya había expuesto ese problema a centenares de sabios, doctores, poetas y escribas, y es este modesto calculista el primero que consigue resolverlo! ¿Cómo fue que llegaste, joven, a la solución? ¿De qué modo podrás demostrar que no había en la solución la menor posibilidad de error?
Interrogado de esa manera por el generoso monarca, el “Hombre que Calculaba” así habló:
- Al formular la primera pregunta: “¿Cuál es el color de tus ojos?”, yo sabía que la respuesta sería fatalmente la siguiente: “Mis ojos son negros”. En efecto. Si ella tenía los ojos negros, diría verdad, es decir, afirmaría: “Mis ojos son negros”. Si tenía los ojos azules, mentiría, y, al responder, diría también: “Mis ojos son negros”. Luego yo afirmo que la respuesta de la primera esclava era única y bien determinada: “Mis ojos son negros”. Hecha, por lo tanto, la primera pregunta, esperé la respuesta que previamente conocía. La esclava, respondiendo en dialecto desconocido, me auxilió de gran manera. Realmente. Alegando no haber entendido el arrevesado idioma chino, interrogué a la segunda esclava: ¿Cuál fue la respuesta dada por tu compañera? La segunda me dijo: “Las palabras de ella fueron: Mis ojos son azules. esa respuesta vino a demostrar que la segunda mentía, pues esa no podía haber sido, de ninguna manera (como ya expliqué) la respuesta de la primera joven. Ahora bien: si la segunda mentía era porque tenía los ojos azules. Repara, ¡oh rey!, en esa notable particularidad para resolver un enigma. De las cinco esclavas había una, en ese momento, cuya incógnita había despejado, con precisión matemática. Era la segunda. Habiendo mentido, tenía los ojos azules. Restaba aún despejar cuatro incógnitas más en el problema.
Aprovechando la tercera y última pregunta, interpelé a la esclava que estaba en el centro de la fila: “¿De qué color son los ojos de las jóvenes que acabo de interrogar?” esta fue la respuesta que obtuve: “La primera tiene los ojos negros y la segunda los tiene azules.” Con respecto a la segunda no tenía duda (como ya expliqué). ¿Qué conclusión pude sacar de la tercera respuesta? Es muy simple. La tercera esclava no mentía, pues afirmaba que la segunda tenía ojos azules. Si la tercera no mentía, sus ojos eran negros. Seguro, ahora, que la primera y la tercera tenían los ojos negros, por exclusión fue fácil saber que las dos últimas los tenían azules (a semejanza de la segunda).
Y el calculista concluyó:
- Puedo afirmar, rey del Tiempo, que en este problema, a pesar que no aparecen fórmulas, ecuaciones o símbolos algebraicos, la solución, por ser exacta y perfecta, debe ser obtenida por medio de un razonamiento puramente matemático.
Estaba resuelto el problema del califa.
En breve, Beremís se vería forzado a resolver otro, mucho más difícil: Telassim, el sueño de una noche en Bagdad.
¡Loado sea Alah, que creó a la Mujer, el Amor y a la Matemática! En la tercera luna del mes de Rhegeb del año 1258, una horda de tártaros y mongoles atacaron la ciudad de Bagdad. Los invasores eran dirigidos por Genghis Can.
El sheik Iezid (Alah lo tenga en su gloria), murió combatiendo junto al puente de Solimán; el califa Al Motacen, se entregó prisionero y fue degollado por los mongoles [142].
La ciudad fue saqueada y duramente arrasada.
La gloriosa Bagdad, que durante quinientos años fuera el centro de la ciencia, las letras y las artes, quedó reducida a un montón de ruinas.
Felizmente yo no asistí a ese crimen que los conquistadores bárbaros practicaron contra la civilización. Tres años antes, después de la muerte del generoso príncipe Cluzir Schá (¡Alah lo tenga en su paz!), seguí para Constantinopla con Beremís y Telassim.
Debo decir que Telassim, antes de su casamiento ya era cristiana, y al cabo de pocos meses logró que Beremís repudiase la religión de Mahoma, y adoptase íntegramente el Evangelio de Jesús Cristo, Salvador.
Beremís quiso ser bautizado por un obispo que supiese Matemática.
Todos los días voy a visitarlo. Llego a veces a envidiar la felicidad en que vive, en compañía de sus hijitos y de su cariñosa esposa.
No queda duda. De todos los problemas, el que mejor resolvió Beremís fue el da la Vida y el del Amor.
Y aquí termina, sin fórmulas y sin números, la historia sencilla de la vida del “Hombre que calculaba”.
- La verdadera felicidad es –según afirma Beremís- poder vivir a la sombra de la religión cristiana. Desde épocas muy remotas, y entre todos los pueblos que cultivaban las ciencias, es probable que se hayan propuesto y resuelto “problemas curiosos”, es decir, problemas que despiertan el interés, ya sea por su enunciado de concepción entretenida, ya por lo ingenioso de las soluciones, o porque la respuesta verdadera no es, generalmente, la primera que se nos ocurre.
Eminentes matemáticos se han ocupado de problemas de esta índole que, además de servir de recreo y entretenimiento, ejercitan la inteligencia del lector y, en consecuencia, lo preparan para resolver, con mayor facilidad, otros problemas que han de presentársele, frecuentemente, en la vida práctica.
Nuestra experiencia en la didáctica de la Matemática nos permite afirmar que la proposición adecuada y resolución de esta índole de problemas en las clases de enseñanza media, constituye un valioso expediente al cual debe recurrir el profesor para hacer sus clases más amables y atrayentes; tan es así, que lo establecen expresamente los programas oficiales de Matemática de la mayoría de las instituciones de enseñanza.
Los autores consultados, entre otros, han sido: Ghersi, Peano, Boucheny, Fourrey, Lucas y Gratz.
Se incluyen en esta colección algunos problemas capciosos; se llama así aquellos cuya verdadera solución no es, generalmente, la primera que se nos ocurre.
El Problema Del Sastre
Un sastre tiene una pieza de paño de 12 metros de longitud, y todos los días corta 2 mts. ¿Al cabo de cuántos días habrá cortado completamente la pieza?
Respuesta. – Evidentemente, en 5 días (y no en 6, como suelen contestar los escolares distraídos).
El Caracol Viajero
Un caracol –por asuntos particulares- desea trasladarse de una huerta a otra, vadeando el muro de separación, que tiene 5 metros de altura; trepa verticalmente por el muro recorriendo cada día 3 metros, y desciende (¡caprichos de caracol!), también verticalmente, cada noche, 2 metros, de modo que cada día avanza, en efectivo, 1 metro de su ruta. ¿En cuántos días llegará a la cima del muro?
Respuesta. – En 3 días (no en 5).
La Tarea De Una Polilla
En un estante se han colocado en forma ordenada, los tres tomos de “La Divina Comedia” de Dante, que constan de 100 páginas cada uno. Una polilla empezó por taladrar la primera hoja del primer tomo y, prosiguiendo horizontalmente en el mismo sentido, dio término a su tarea con la última hoja del último tomo. ¿Cuántas hojas taladró?
Respuesta. – 102 hojas, puesto que los volúmenes e hallan ordenados de izquierda a derecha, y las hojas de los volúmenes resultan ordenados de derecha a izquierda; y además, por hallarse adyacentes al segundo tomo, la primera hoja del primero, así como la última del tercero.
La Cabellera Humana
Demostrar que en una ciudad de 130.000 habitantes existen, por lo menos, dos personas con igual número de cabellos.
En efecto: un individuo –por cierto muy paciente y que poco tenía que hacer- contó y calculó que cada centímetro cuadrado del cuero cabelludo humano contiene, al máximo, 165 cabellos. Como la superficie referida de la cabeza humana es de unos 775 cm2, el número máximo de cabello que podrá tener una persona será 775 X 165, o sea, 127.875. podrá existir, pues, una persona con 1 cabello, otra con 2, otra con 3… , y así sucesivamente, hasta una última con el máximo de 127.875 cabellos. Como el número 130.000 es mayor que 127.875, podremos afirmar, pues, que por cada 130.000 habitantes debe repetirse un mismo número de cabellos, en otra cabeza.
Una Familia Numerosa Compuesta De Pocas Personas
Cierta familia está constituida por: un abuelo, una abuela, un suegro, una suegra, un yerno, tres hijas, cuatro hijos, dos padres, dos madres, tres nietos, dos nietas, cuatro hermanos, tres hermanas, dos cuñados, dos maridos, dos esposas, un tío, tres sobrinos y dos sobrinas. ¿En total 40 personas? No, solamente son 10. ¿Cómo está formada esa familia?
A continuación damos el cuadro genealógico:
Una señora, bastante ingenua, entrega a un joyero una cruz de brillantes (representada en la figura a), haciéndole notar que conoce el número de brillantes que contiene, puesto que contándolos a partir de uno cualquiera de los extremos superiores hasta la parte inferior de la cruz, cuenta siempre nueve; pero el joyero, poco escrupuloso, se apropia de dos de los brillantes y le devuelve la cruz modificada de modo que la ingenua señora, efectuada la verificación en la forma acostumbrada, no se da cuenta del engaño. ¿Cuál es el truco usado por el joyero?
La respuesta se evidencia en la (figura b) que da una suma total de 13 brillantes en lugar de 15.
Un juntaduchos puede liar un cigarrillo con 3 puchos. Tiene 10. ¿Cómo logra fumar 5 cigarrillos?
Con los 10 puchos lía 3 cigarrillos y le sobra 1 pucho.
Fuma 3 cigarrillos, y tiene luego 4 puchos, con 3 de los cuales lia un cuarto cigarrillo que fuma, y tiene entonces 2 puchos.
Pide prestado 1 pucho a un amigo, lia un quinto cigarrillo, lo fuma, y devuelve el pucho prestado (como persona honrada que bien puede serlo el juntapuchos).
Ha fumado, pues, 5 cigarrillos.
Problema de la Mosca y la Araña
La (figura a) representa un salón, de piso rectangular, que tiene 20 metros de largo, 10 metros de ancho y 10 metros de alto.
Una mosca se encuentra en un punto M, en el eje vertical de la pared del frente, a un metro de distancia del techo; una araña se encuentra en el punto A, en el eje vertical de la pared del fondo, a un metro de distancia del piso. ¿Cuál es el camino más corto que deberá seguir la araña para atrapar la mosca? (Se sobreentiende que la trayectoria debe realizarse sobre paredes, piso o techo).
La solución que primeramente se le ocurrirá a la generalidad de las personas, es la línea quebrada AQPM trazada siguiendo los ejes de las paredes del fondo y del frente, también el del piso; la medida de esta trayectoria resulta de 1 + 20 + 9 = 30 metros.
En la orilla de un río se encuentra un lobo, una cabra y un gran repollo; no hay más que un barquichuelo tan pequeño, que únicamente da cabida al barquero y a una sola de tales cosas. ¿En qué forma puede hacerse la travesía para evitar que el lobo se coma la cabra, o ésta al repollo, durante la ausencia del barquero?
Designemos con L, C, R, el lobo, la cabra y el repollo, respectivamente. Al partir tenemos:
PRIMERA ORILLA | SEGUNDA ORILLA | |||||
L | C | R | . | . | . | |
A continuación indicamos como deberá el barquero efectuar los sucesivos pasajes:
I. – Transportará primeramente la cabra:
L | . | R | . | C | . |
II. - En el segundo viaje transportará el lobo, pero regresará con la cabra; dejará a esta en la primera orilla y transportará el repollo:
. | C | . | L | . | R |
III. - Regresará finalmente para transportar la cabra:
. | . | . | L | C | R |
NOTA . – Otra solución se obtiene si, en el pasaje II, en lugar de transportar primeramente el lobo y luego el repollo, se transporta primeramente el repollo y luego el lobo.
Los Tres Maridos Celosos
Tres maridos se encuentran con sus respectivas mujeres ante un río que se proponen atravesar. Solo disponen de una pequeña embarcación sin barquero, apta para transportar únicamente dos personas a la vez. ¿Cómo estarán esas seis personas de manera que ninguna mujer quede en compañía de dos hombres, si su marido no está presente?
Este problema esa antiquísimo, y no es más que la generalización del anteriormente tratado, de la travesía del barquero.
Designemos A, B, C, a los maridos celosos y con a, b y c, sus mujeres respectivas. A la partida se tiene:
PRIMERA ORILLA | SEGUNDA ORILLA | |||||
A | B | C | . | . | . | |
a | b | c | . | . | . | |
A continuación indicamos como deben efectuarse los sucesivos pasajes:
I. – Pasan primeramente dos mujeres:
A | B | C | . | . | . | |
. | . | c | a | b | . |
II. – Una mujer regresa y se lleva a la tercera:
A | B | C | . | . | . | |
. | . | . | a | b | c |
III. – Regresa una mujer, se queda con su marido, y luego pasan los otros dos maridos:
. | . | C | A | B | . | |
. | . | c | a | b | . |
IV. – Un marido regresa con su mujer, a la que deja, y se lleva al otro marido:
. | . | . | A | B | C | |
. | b | c | a | . | . |
V. – La mujer a, única que se encuentra en la segunda orilla, se encarga finalmente de la conducción sucesiva de las otras dos, o bien, después de conducir a una de ellas, cede la embarcación al marido de la tercera, que se encarga de su conducción.
Los Tres Blancos y los Tres Negros
Tres blancos y tres negros se proponen cruzar un río; los tres blancos saben remar, y, de los negros, sólo un. El bote es de capacidad para dos personas. En ambas orillas tiene que haber siempre mayoría de blancos, o igualdad, peor nunca superioridad de negros. ¿Cómo realizar la travesía?
A continuación indicamos, esquemáticamente, los 14 viajes simples que debe realizar el bote. Los tres círculos señalan los hombres blancos y los tres puntos, los negros; hemos recuadrado el punto que indica el negro que sabe remar; las flechas indican el sentido del viaje, así como el hombre que lo realiza.
En Koenisberg (Pomerania) existe una isla llamada Kueiphof; el río la rodea y divide en dos brazos, sobre los cuales están tendidos siete puentes a, b, c, d, e, f, g. ¿Será posible realizar un paseo atravesando no más de una vez todos los puentes?
La notación A B D indicará tanto el camino A a B f D como el A b B f D; si se pasa por dos puentes tendremos que emplear, pues, tres letras para designar el camino.
Desde la época de la construcción de dichos puentes (año 1759), insignes matemáticos se ocuparon del problema, llegando a la conclusión que sería necesario construir otro puente para que el problema tuviera solución.Cuéntase que un habitante de dicha ciudad se propuso resolverlo, prácticamente, recorriendo de todas maneras posibles los siete puentes, pero, como en el recorrido se hallaba un manicomio, parece que tuvieron que recluir en él al perseverante pomerano.
Evidentemente que con la sola experimentación resultará muy laborioso juzgar sobre la posibilidad o imposibilidad de resolver esta clase de problemas, pertenecientes a los llamados de geometría de posición; en ellos resulta generalmente más fácil de demostrar la imposibilidad que la posibilidad.
Como en el problema de los siete puentes de Koenisberg son los 5 los que conducen a la región A y 3 los que conducen a cada una de las regiones B, C y D, en la anotación del recorrido completo la letra A deberá aparecer tres veces, y cada una de las otras tres letras deberá aparecer 2 veces, en total: 3+2+2+2 = 9 letras, y no 8, como habíamos hallado antes. No existe, pues, posibilidad de resolver el problema propuesto.
Para el problema en cuestión, llamemos A, B, C, D, las diversas regiones separadas por los brazos del río.Si se pasa de la región A a la B, ya sea por intermedio del puente a, o del b, es decir franqueando un puente, designaremos el camino por AB, o sea, con dos letras; la primera letra indica la región de partida, y la segunda, la de llegada.
La notación A B D indicará tanto el camino A a B f D como elA b B f D; si se pasa por dos puentes tendremos que emplear, pues, tres letras para designar el camino.
Si se pasa de la región A a la B, de ésta a la D, y finalmente a la C, designaremos el camino A B C D; es decir, que pasando por tres puentes, tendremos que emplear cuatro letras para designar el camino.
Observemos que el número de letras que designa un camino excede en 1 al de puentes a franquear. Para el problema de los 7 puentes de Koenisgberg, todo camino posible deberá designarse, pues, con 8 letras.
Estas 8 letras deberán estar dispuestas de modo que la sucesión de letras A y B, o sea, A B o B A, se presente dos veces; análogamente para la sucesión de letras A y C. En cambio la sucesión de letras B y D, o la de C y D se presentará una sola vez, porque las regiones que representan están unidas por un solo puente.
El problema se reduce, pues, a formar con las cuatro letras A, B, C, D, una sucesión de 8 letras en la que aparezcan las sucesiones binarias referidas tantas veces como hemos indicado. Pero antes de buscar tal disposición investiguemos si ello es posible.
Consideremos, por ejemplo, la región A; si ella estuviese unida a la B mediante un puente a, el viajero que lo atravesara, o se encuentra en A antes de pasar, o se encontrará después; por consiguiente, tanto en un caso como en el otro, la letra A deberá figurar una sola vez en la anotación. Supongamos ahora que sean tres puentes a, b, c que conduzcan a la región A; si el viajero atraviesa los tres puentes, la letra A aparecerá dos veces en la anotación. Análogamente, si cinco puentes conducen a la región A, esta letra figurará tres veces en la anotación del paso a través de todos los puentes.
Como en el problema de los siete puentes de Koenisberg son los 5 los que conducen a la región A y 3 los que conducen a cada una de las regiones B, C y D, en la anotación del recorrido completo la letra A deberá aparecer tres veces, y cada una de las otras tres letras deberá aparecer 2 veces, en total: 3+2+2+2 = 9 letras, y no 8, como habíamos hallado antes. No existe, pues, posibilidad de resolver el problema propuesto.
A continuación presentamos otro caso de cruce de puentes, pero cuya solución es posible; una de ellas es la siguiente:
D l E q B p A n E m A k D i C h A g C f F e A d F c B b F a E
Figuras de un Solo TrazoEl problema de los siete puentes, que tratamos recientemente, se puede representar, esquemáticamente, con la (figura a).
En dichas figuras llamaremos nudos a los puntos como A, B, C,… de los cuales parten los trazos los trazos de líneas que unen un nudo con otro.
Figura b, Figura c y Figura d
Se llama orden de un nudo al dado por el número de trazos que de él parten; así, por ejemplo, el orden del nudo A es 5, el de B es 3.Si logramos recorrer toda una figura compuesta de líneas, ya sea en el plano o en el espacio, mediante un solo trazo, volviendo al punto de partida, decimos que hemos recorrido un circuito cerrado. La posibilidad de realización de tal circuito está sujeta a las siguientes condiciones:
Las figuras que no tienen nudos de orden impar se pueden dibujar con un trazo continuo partiendo de un nudo cualquiera (figuras b, c, d).
La (figura b) representa el pentágono regular estrellado, símbolo que empleaban los pitagóricos para reconocerse (siglo V antes de Cristo).
La (figura c) representa la firma de Mahoma, formada por dos medias lunas opuestas, y que, según la tradición, trazaba el Profeta con la punta de su cimitarra.
La (figura d) es un heptágono con todas sus diagonales. En general, todo polígono de un número impar de lados, con sus respectivas diagonales, es una figura de circuito cerrado, mientras que no lo es, si tiene un número par de lados.
Como otro ejemplo interesante, si se dividen los tres lados del triángulo en un mismo número cualquiera de partes iguales, y se unen los puntos de división correspondientes por rectas paralelas a los lados, se obtiene una figura que no contiene más que nudos de orden par, y se puede describir, pues, con un solo trazo.
Cuando una figura tiene solamente dos nudos impares, puede describirse con trazo continuo partiendo de uno de dichos nudos.
Así, por ejemplo, la (figura f) puede describirse en cualquier sentido con tal que se parta de uno de sus nudos impares B o D.
Las figuras (g, h, i) se hallan en las mismas condiciones; la (figura i) solo contiene los dos nudos impares A y Z.
Figura f, Figura g y Figura h
Dibujando en grande sobre una hoja de cartón esta última figura, puede realizarse un juego interesante. Se colocan luego fichas pequeñas sobre el centro de todas las líneas que unen los puntos contiguos; el juego consiste en determinar el recorrido a seguir para levantar todas las fichas sucesivamente.
Figura l
Las figuras que tienen más de dos nudos impares no pueden describirse con un trazo continuo.Puede agregarse que, si una figura tiene (2n) nudos impares, puede describirse completamente mediante (n) recorridos diferentes.
Figura k, Figura m y Figura n
Así, por ejemplo, las (figuras k, m, n) presentan el caso de imposibilidad que hemos señalado. La (figura k) se puede describir mediante dos recorridos, porque tiene cuatro nudos impares; la (figura m), que tiene ocho nudos impares, mediante cuatro recorridos, y la (figura n), que tiene doce nudos impares, mediante seis recorridos.
NOTA . – Es posible dibujar, con un solo trazo, si empleamos un ingenioso artificio, el cuadrilátero con sus dos diagonales, indicado en la (figura k).
En efecto, sea A B C D (figura p) la hoja de papel que emplearemos para el trazado. Rebatimos la parte superior efectuando un doblez por E F (figura q).
Trazamos entonces el lado 1 del cuadrilátero sobre el frente del papel, y prolongamos este lado sobre el dorso; continuamos por 2, 3 sobre el dorso y prolongamos el lado 3 sobre el frente.
Rebatiendo entonces la parte superior de la hoja (figura r), trazamos sucesivamente sobre el frente las rectas 4, 5, 6, 7. Obtenemos así, mediante un trazo continuo, un cuadrilátero y sus diagonales.
Figura p, Figura q y Figura r
El Primero en Contar 100
De dos personas, una dice un número de 1 á 10, y la otra agrega un número, siempre de 1 á 10; la primera agrega un número entre los mismos límites, y así sucesivamente. La primera que llega a decir 100, gana. ¿Cómo se logra ganar?
La primera que dice 89 podrá, en su adición sucesiva, decir 100; para lograr decir 89, basta decir uno de los siguientes números: 78, 67, 56, 45, 34, 23, 12 ó 1.
Par o Impar
Un amigo tiene en una mano un número par de monedas u otros objetos, y en la otra un número impar; adivinar en que mano se encuentra el número par de monedas.
Hágase multiplicar el número de monedas contenidas en la mano derecha por un número par cualquiera (que elegirá el amigo), las de la mano izquierda por un número impar, y hágase sumar los dos productos.
Si la suma que dirá el amigo es impar, el número par de monedas está en la mano derecha.
Si la suma es par, el número par está en la mano izquierda.
La explicación de este juego es la siguiente:
El producto de un número cualquiera (par o impar) por un número par, es un número par.
Si el número correspondiente a la mano izquierda es impar, su producto por un número impar es impar, y la suma de los dos productos (par más impar) es impar.
Por el contrario, si el número correspondiente a la mano izquierda es par, su producto por un número impar es par, y la suma de los productos (ambos pares), es par.
A continuación esquematizamos la explicación que precede:
Disponga sobre una mesa de tres objetos diferentes (por ejemplo, un anillo, un reloj, un cigarrillo) y 24 fichas, o fósforos.
Ruegue a tres personas de tomar, cada una de ellas, uno de los objetos, sin que usted sepa cual ha tomado. De a la persona A una ficha, a la B dos y a la tercera C tres, y deje sobre la mesa las 18 restantes. Pase luego a otra sala., desde donde rogará a la otra persona que posee el anillo que tome tantas fichas como las que tenga; a la del reloj que tome el doble de las que ha recibido, y a la del cigarrillo cuatro veces cuantas ha recibido.
Volviendo a la sala, cuente entonces (en la forma más disimulada posible) cuantas fichas quedan de las 18; podrá así adivinar quién tomó uno u otro de los objetos:
Los 6 casos posibles de repartición de las 6 primeras fichas entre las tres personas son:
Anillo | Reloj | Cigarrillo |
1 | 3 | 2 |
Es decir, que la persona a quien dimos una ficha, o sea la A, tiene el anillo; a quien dimos 2, o sea la B, tiene el cigarrillo, y a quien dimos 3, o sea la C, tiene el reloj.
Adivinar La Edad De Una Persona
Se empieza por calcular la diferencia entre la edad de la persona y la de usted:
1. si la persona es de más edad que la de usted:
Al número 99 réstele su edad.
Pídale a la persona que agregue a la edad que ella tenga, el número que expresa dicha resta.
La suma que ella halará es un número evidentemente superior, o igual a cien. Haga eliminar de ese número la cifra de las unidades.
La suma obtenida, que usted solicitará diga la persona, es la diferencia de las dos edades. Agregará usted, pues, esa diferencia a su edad, y tendrá así la de la persona.
Así, por ejemplo, sea su edad A = 19 años y la de la persona cuya edad se propone adivinar, B = 46.
Usted resta mentalmente 19 de 99 y obtiene 80.
Usted hace agregar 80 á 46, lo que da 126.
Luego hace usted eliminar la cifra 1 de las centenas de 126 y la hace agregar á 26, lo que da 27, que es la diferencia de las edades: B – A = 46 – 19 = 27.
El resultado obtenido se explica fácilmente; en efecto: Usted empezó por restar a 99 su edad, obteniendo 99 – A, diferencia que hizo agregar a la edad de la persona, obteniendo B + 99 – A.
De este número usted hizo eliminar la cifra de las centenas, o sea, restó 100, y luego agregó una unidad simple, es decir, que restó 99; quedó, pues, (B + 99 - A) – 99 = B – A.
2. Si la persona es de menos edad que la de usted, se procede como antes hasta la segunda faz de la operación; luego, como la suma que se obtiene no llega a 100, usted hace agregar a ella un número ficticio a fin de encontrar una suma mayor que 100. se continúa como en el caso anterior, y la suma que le dirá la persona la restará usted de aquel número ficticio, siendo el resultado la diferencia de las dos edades.
Así, por ejemplo, si su edad es A = 29 años y la de la persona B = 23, la diferencia de su edad con 99 es 70, que hace agregar a 23, obteniendo 93.
Luego hace agregar un número ficticio, por ejemplo 30, obteniendo 123; se elimina la cifra 1 de las centenas, que se agrega como unidad simple a 23, obteniendo 24; la diferencia de edades es 30 – 24 = 6.
Este resultado se explica en forma análoga al anterior; en efecto, con las mismas notaciones, y llamando N al número ficticio empleado en el juego, las fases del mismo son las siguientes:
N – [(B + 99 – A + N) - 99] = N – (B – A + N) = A – B
Juego Del AnilloUn amigo (o amiga) se coloca, secretamente, un anillo. Adivinar en que mano, en que dedo y en que falange.
Para ello designemos la mano derecha con el número 1 y la izquierda con el 2; los dedos con los números 1, 2, 3, 4, 5, empezando por la más próxima a la mano, pero correspondiendo al pulgar solamente los números 1 y 2.
El problema se reduce, pues, a adivinar tres números que no exceden de 5.
Para fijar ideas, supongamos que el amigo ha colocado el anillo en la mano izquierda (2), en el tercer dedo (3), y en la primera falange (1). Las operaciones a realizar son las siguientes:
1. Que el amigo efectúe, en secreto:
El doble del primer número y le sume la unidad: | 2 x 2 + 1 = 5 |
El producto de este resultado por 5: | 5 x 5 = 25 |
La suma de este resultado con el segundo número: | 25 + 3 = 28 |
El doble de este número y le sume la unidad: | 28 x 2 + 1 = 57 |
El producto de este resultado por 5: | 57 x 5 = 285 |
La suma de este resultado con el tercer número: | 285 + 1= 286 |
2. De este número, que nos dirá el amigo, restamos 55, obteniendo la diferencia:
286 – 55 = 231
cuyas cifras 2, 3, 1 son, respectivamente, los números que nos proponíamos adivinar.DEMOSTRACIÓN . Para justificar este juego llamemos b, c, respectivamente, los números a adivinar.
Observemos que las operaciones realizadas con estos números, en el orden anteriormente indicado, son las siguientes:
a x 2+1; (2ax + x + 1) x 5; 10a + 5 +b;
(10a + 5 + b)2 + 1; (20ª + 11+ 2b)5; 100 a +55 + 10b + c
100a +55 + 10b + c = 100a + 10b + c
El número que expresa esta suma tiene, precisamente, como cifras de las centenas de las decenas y de las unidades, a, b y c respectivamente.Este juego resulta aún más interesante realizándolo en una reunión de varias personas, y, adivinando, además, cuál de ellas se ha colocado el anillo; el número de personas que pueden intervenir en el juego no debe exceder de 9.
Se empieza por numerar cada persona: a la primera se le asignará el número 1, a la segunda 2, a la tercera 3, etc.; cada persona deberá recordar su número.
El problema se reduce, pues, a adivinar 4 números que no exceden de 9.
Con las mismas convenciones que ya indicamos para el caso que el juego se realice con una sola persona, se rogará que una de ellas se coloque el anillo. Se sobreentiende que, en ese momento, convendrá dar la espalda al grupo de personas que intervienen en el juego. Luego se rogará a otra persona que, en posesión del secreto del número de la persona que posee el anillo, así como del número de la mano, dedo y falange donde se ha colocado el anillo, efectúe las siguientes operaciones:
Duplique el primer número (el de la persona) y sume 1 al resultado; multiplique por 5 y agregue el segundo número (el de la mano).
Duplique el resultado, sume 1, multiplique por 5 y agregue el tercer número (el del dedo).
Duplique el resultado, sume 1, multiplique por 5 y agregue el cuarto número (el de la falange).
De este número, que nos dirá el amigo, restamos 555; la cifra de los millares de este resto será el primer número que nos proponemos adivinar (el de la persona); la cifra de las centenas, el segundo número (el de la mano), y así sucesivamente.
Tabla Misteriosa
Con las cinco filas de números siguientes, podemos adivinar el número que habrá pensado una persona, desde 1 hasta 31, sabiendo solamente en cuáles de las filas se encuentra.
1.ª | 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | 25 | 27 | 29 | 31 | … |
2.ª | 2 | 3 | 6 | 7 | 10 | 11 | 14 | 15 | 18 | 19 | 22 | 23 | 26 | 27 | 30 | 31 | … |
3.ª | 4 | 5 | 6 | 7 | 12 | 13 | 14 | 15 | 20 | 21 | 22 | 23 | 28 | 29 | 30 | 31 | … |
4.ª | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | … |
5.ª | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | … |
El número pensado es la suma de los primeros números de las filas donde se encuentra. Así, por ejemplo, si nos dice que el número pensado se encuentra en las filas 1.ª, 3ª. y 4ª., será: 1 + 4 + 8 = 13; si está en la 3ª. Y 5ª., será: 4 + 16 = 20.
La tabla que hemos limitado en el número 31, se construye así: la 1ª. fila está formada por la sucesión de los primeros números impares; cada fila de las siguientes empieza con las potencias sucesivas de 2.
La 2.ª fila se obtiene sumando al primer número de ella, sucesivamente, el primero de la fila siguiente, o sea, sumando 4, obteniendo 2 + 4 = 6, 6 + 4 = 10, …, 14, 18, 22, 26, 30, y disponiendo esos números cada dos lugares, para intercalar luego el número consecutivo a cada uno de dichos números, hasta completar los lugares disponibles; es decir, al 2 seguimos el 3; al 6 seguimos el 7, etc.
La 3ª. fila se obtiene sumando al primer número de la misma, sucesivamente, el primero de la fila siguiente, o sea: 4 + 8 = 12, 12 + 8 = 20, …, y disponiendo esos números consecutivos a cada uno de ellos, hasta completar los lugares disponibles; es decir, al 4 seguimos el 5, 6, 7; al 12 seguimos el 13, 14, 15; … etc.
La 4ª. fila se obtiene análogamente, es decir, sumando sucesivamente 16, obteniendo así, 24, 40, …, y disponiendo esos números cada ocho lugares, e intercalando luego los números consecutivos al 8, al 24, … etc.
La 5ª fila se forma análogamente.
Si el número a adivinar es mayor que 31, será necesario prolongar la tabla más allá de dicho número, debiendo entonces agregar, también, nuevas filas.
La Multiplicación Musulmana
Resulta curiosa la disposición adoptada por los musulmanes para la multiplicación, tal vez más fácil de comprender, por los principiantes, que la nuestra. Sea, por ejemplo, 5817 x 423.
Escribimos uno de los factores, 5817, de izquierda a derecha, y el otro, 423, de abajo para arriba; trazamos una cuadrícula, así como sus diagonales, como indica la figura.
Así, efectuaremos: 3 x 5 = 15; escribimos 1 debajo de la diagonal de la primera casilla, y 5 arriba. 3 x 8 = 24; escribimos 2 debajo y 4 encima de la diagonal de la segunda casilla, y así sucesivamente.
Se efectúan luego las sumas de las cifras adyacentes a una misma diagonal, en forma análoga a nuestra multiplicación; el número 2460591 así obtenido es el producto de los números dados.
Multiplicación Fulmínea
Resulta interesante el procedimiento de multiplicación de dos números de varias cifras indicado por insignes matemáticos, como Fourier, en 1831, Cauchy, en 1840, y otros, en el que se procede de izquierda a derecha.
Se multiplican las cifras que se hallan en la misma vertical, se suman sus productos y se escriben estas sumas en forma escalonada, a la derecha. Finalmente se suman esos números como indica el esquema.
Así, diremos: 4 x 5 = 20, y escribimos 20 a la derecha; 4 x 8 = 32, 2 x 5 = 10; sumando estos productos tenemos 32 + 10 = 42, y escribimos 42 a la derecha, en forma escalonada,… etc.
Multiplicación Rusa
Algunos pueblos de Rusia multiplican sin emplear la tabla pitagórica.
Hecho esto se tachan de la columna de la derecha todos los números colocados enfrente de los números pares de la otra columna y se suman los números no tachados; esta suma será el resultado de la multiplicación: 22 x 6 = 132.
OPERACIONES DE RESULTADOS NOTABLES
El matemático Árabe Ibn Albania (siglo XII), publicó las siguientes operaciones curiosas:9 x 9 + 7 = 88 | 11 x 11 = 121 |
98 x 9 + 6 = 888 | 111 x 111 = 12321 |
987 x 9 + 5 = 8888 | 1111 x 1111 = 1234321 |
9876 x 9 + 4 = 88888 | 11111 x 11111 = 123454321 |
98765 x 9 + 3 = 888888 | 111111 x 111111 = 12345654321 |
987654 x 9 + 2 = 8888888 | 1111111 x 1111111 = 1234567654321 |
9876543 x 9 + 1 = 88888888 | 11111111 x 11111111 = 123456787654321 |
98765432 x 9 + 0=888888888 | 111111111 x 111111111=12345678987654321 |
1 x 9 + 2 = 11 | 1 x 8 + 1 = 9 |
12 x 9 + 3 = 111 | 12 x 8 + 2 = 98 |
123 x 9 + 4 = 1111 | 123 x 8 + 3 = 987 |
1234 x 9+5 = 11111 | 1234 x 8 + 4 = 9876 |
12345 x 9 + 6 = 111111 | 12345 x 8 + 5 = 98765 |
123456 x 9 + 7 = 1111111 | 123456 x 8 + 6 = 987654 |
1234567 x 9 + 8 = 11111111 | 1234567 x 8 +7= 9876543 |
12345678 x 9 + 9 = 111111111 | 12345678 x 8 + 8= 98765432 |
123456789 x 9 + 10 = 1111111111 | 123456789 x 8 + 9 = 987654321 |
El Número 12345679
Este número está formado por la sucesión de las cifras significativas, excepto el 8. Si se le multiplica por uno cualquiera de los términos de la progresión aritmética:
9; 18; 27; 36; 45; 54; 63; 72; 81
el producto se compondrá de 9 cifras iguales. Así tenemos:12345679 x 9 = 111111111
12345679 x 18 = 222222222
12345679 x 27 = 333333333
…
12345679 x 81 = 999999999
Diversas Maneras de Escribir 100a. Agrupar la sucesión de las nueve cifras significativas mediante los signos de sumar o restar, de modo que el resultado sea 100.
RESPUESTA : 123 – 45 – 67 + 9 = 100
b. Con los nueve primeros números naturales sin repetir, empleando signos aritméticos, escribir dos expresiones de 100.
RESPUESTA :
100 = 97 + 1/2 + 6/4 + (3+5)/8 = 75 + 24 + 3/6 + 9/18
a. Con cinco cifras iguales escribir, de varias maneras el número 100.
RESPUESTA :
Empleando el 1: 111 - 11
Empleando el 3:33 x 3 + 3/3
Empleando el 5:5 x 5 x 5 – 5 x 5
Empleando el 5:(5 + 5 + 5 + 5) x 5
INVERSIÓN DE NÚMEROS
Los Números de 3 Cifras Decrecientes en 1 y el Número 198.Escríbase un número de tres cifras decrecientes en 1, por ejemplo, 765; inviértanse las cifras: 567; efectúese la resta de esos dos números: 765 – 567 = 198. Se obtendrá siempre el mismo número, 198.
Este resultado se explica fácilmente. En efecto, si n es la cifra de las unidades del número dado la de las decenas es n+1 y la de las centenas, n+2.
Expresando dicho número mediante sus unidades simples, resulta:
100(n + 2) + 10(n + 1) + n
Análogamente, para el número que se obtiene al invertir las cifras del primero, resulta:100 n + 10(n + 1) + (n + 2)
restando de la primera expresión esta última, tenemos:100n + 200 + 10(n + 1) + n – 10 n – 10(n + 1) - n – 2 = 200 – 2 = 198
Los Números de 3 Cifras y el Número 1089Escríbase un número de tres cifras, la primera y la última diferentes, por ejemplo, 825; inviértase el orden de las cifras, 528, y luego efectúese la resta de esos dos números: 825 – 528 = 297.
Agréguese a esta diferencia el número que resulta de invertir sus cifras: 297 + 792 = 1089. Se tendrá siempre el mismo número, 1089.
Para explicar este resultado, sean a, b, c las cifras de las centenas, decenas y unidades simples, respectivamente, y supongamos sea a mayor que c; tendremos:
El número elegido es 100a + 10b + c.
El número invertido es 100c + 10b + a.
Restando del primer número el segundo, tenemos:
100(a – c) + c – a,
que puede escribirse así:100 (a – c – 1) + 90 + (10 + c – a)
El número invertido será, pues:100 (10 + c – a) + 90 + (a – c – 1)
y sumando estas dos últimas expresiones, resulta:100 (10 – 1) + 90 + 90 + 10 – 1 = 1089
LOS CUADRADOS MÁGICOSSi dividimos un cuadrado en cierto número de casillas, también cuadradas, y en cada una de ellas colocamos un número, sin repetición, de modo de obtener siempre la misma suma en cada fila, en cada columna y también en cada diagonal, se tendrá así un cuadrado mágico.
6 + 1 + 8 = 7 + 5 + 3 = 2 + 9 + 4 = 15
Sumando en columnas verticales:6 + 7 + 2 = 1 + 5 + 9 = 8 + 3 + 4 = 15
Sumando en diagonal:6 + 5 + 4 = 8 + 5 + 2 = 15
Los antiguos Magos de Persia eran médicos, pretendían curar enfermedades aplicando a la parte enferma un cuadrado mágico, siguiendo el conocido principio de medicina: primum non nocère, o sea, primer principio: no dañar.El número de filas, y, en consecuencia, de columnas que tiene un cuadrado mágico se llama orden del mismo. La suma constante de los números de una fila, o de una columna o de una diagonal se llama constante del cuadrado mágico. En el ejemplo anterior el orden es 3, y la constante 15.
No puede formarse un cuadrado mágico de orden 2.
Cuadrados Mágicos Impares
(Son los de orden impar). - Para construir un cuadrado mágico impar, por ejemplo de orden 5, se empieza por construir un cuadrado A B C D con 25 casillas, (figura b); luego, sobre cada lado, que ya tiene 5 casillas, se agregan, en este caso, filas de 3 y de 1 casilla. Se escribe entonces en la casilla más alta el número 1, y descendiendo hacia la derecha, en el sentido diagonal, los números 2, 3, 4, 5. Después de esto se escribe 6 en la casilla situada a la izquierda y debajo del 1, siguiendo en diagonal, 7, 8, 9, 10. Luego, siguiendo siempre el mismo procedimiento, se escriben los números 11, 12, 13, 14, 15, que completan una diagonal; análogamente, 16, 17, 18, 19, 20, y finalmente, 21, 22, 23, 24, 25.
Todo número, sin salir de su columna vertical o fila horizontal, se colocará en la casilla vacía más alejada de la que ocupa, cuidando de comenzar la operación por las bandas adicionales más próximas al cuadrado .
En la (figura c) presentamos el cuadrado mágico de orden 5 así obtenido.
Cuadrados Mágicos Pares
(Son los de orden par). - Estos cuadrados son generalmente difíciles de construir, salvo el de orden 4. Para este caso disponemos en un cuadrado de 16 casillas, y, en su orden natural, los 16 primeros números, (figura d). Dejando luego fijos los números de las diagonales, permutamos entre si los otros ocho de la forma indicada en la (figura e). El cuadrado obtenido, (figura f), será mágico, siendo su módulo 34.
Se llaman así a los cuadrados mágicos que, además de tener una suma constante en los 2 ( n + 1 ) modos habituales modos habituales de sumar, siendo n el orden del cuadrado, se puede obtener dicha suma de muchos otros modos, regulares o geométricos.
Figura h
Diagramas Geométricos
De Cuadrados MágicosSi en un cuadrado mágico unimos con rectas los números que lo forman en su orden natural, se obtiene una línea poligonal, que tiene como extremos el número menor y el mayor, respectivamente; dicha poligonal caracteriza al cuadrado.
Así, por ejemplo, para el cuadrado mágico de orden 3, (figura a), obtenemos el diagrama geométrico que indicamos en la (figura i).
Otro diagrama geométrico interesante es el del cuadrado mágico de orden 8, dibujado en la (figura k).
PARADOJAS MATEMÁTICAS
Se llaman paradojas matemáticas ciertos resultados notoriamente falsos que parecen deducirse de demostraciones rigurosas, pero durante las cuales se ha efectuado una operación que no tiene sentido, o un razonamiento erróneo, o, aún, una construcción geométrica cuyo trazado no es correcto.Primera Paradoja: 1 = 2.
Sean dos números iguales, a y b; escribimos: b = a.
Multiplicando los dos miembros de esta igualdad por el mismo número a, tenemos:
b x a = a2
restando a ambos miembros el mismo número b2, resulta,b x a – b2 = a2 – b2
que puede escribirse así:b x (a – b) = (a + b) x (a – b)
Dividiendo los dos miembros por (a – b), tenemos,b = b + b, o sea, b = 2 b, de donde, 1 = 2.
Este resultado paradojal se explica fácilmente. En efecto, pueden dividirse los dos miembros de una igualdad por un mismo número con la condición que ese divisor sea diferente de cero. Pero en el ejemplo tratado hemos dividido los dos miembros de una igualdad por ( a – b) que, por hipótesis, es una cantidad nula, operación ilícita que nos condujo al resultado absurdo: 1 = 2.Segunda Paradoja
En todo triángulo rectángulo, cada lado es igual (?) a la suma de los otros dos.
Sea el triángulo ABC (figura a) y M, N, P, los puntos medios de sus lados; tracemos las rectas MP y NP.
AN + NP + PM + MB = AC + CB
Efectuando una construcción análoga para los triángulos ANP, PMB, y continuando de ese modo indefinidamente, vemos que las líneas quebradas sucesivamente formadas tienen siempre su longitud igual a ( AC + CB). Como la longitud de los segmentos que forman la línea quebrada disminuye constantemente, y sus vértices se aproximan cada vez más a la recta AB, decimos que en el límite, el perímetro de las líneas quebradas llega a confundirse con AB, y, por consiguiente, AB= AC + CB .Esta paradoja se explica por la falsa interpretación del término “límite”, cuya definición correcta es: “Decimos que una magnitud variable x tiende hacia un límite determinado A, si los valores sucesivos de x se aproximan al número A de modo que el valor absoluto de la diferencia (x - A) pueda llegar a ser menor que todo el número positivo dado, por pequeño que este sea”.
En el ejemplo tratado, x y A son, respectivamente, el perímetro de las líneas quebradas y la longitud del lado AB. Pero x es constante y no variable, y la diferencia (x – A) es también constante. No siendo lícito aplicar la noción de límite a magnitudes que no satisfacen las condiciones de la definición precedente, no es de extrañarse, pues, que en el caso tratado se haya llegado a un resultado absurdo.
Tercera Paradoja
Con un razonamiento análogo al de la paradoja anterior puede establecerse que una semicircunferencia es igual (?) a su diámetro.
Para ello se trazan dos semicircunferencias (figura b) que tengan por diámetros los radios OA = OB = R de una semicircunferencia dada. Esta última tiene por longitud pR, y la suma de las otras dos es:
π * R/2 + π * R/2 = π * R
o sea, igual a la primera.Continuando con la misma construcción indefinidamente, se tiene siempre la misma longitud pR para la línea formada por las 4, 8, 16, … semicircunferencias, las que, por ser cada vez menores, nos inducen a decir que forman una línea que se confunde con el diámetro AB, o sea, pR = AB.
Cuarta Paradoja
Por un punto exterior a una recta se pueden trazar dos (?) perpendiculares a dicha recta.
Consideremos dos circunferencias (figura c) de centros O y O’, que se cortan en A y B.
El ángulo AFC, por ser inscrito en un semicírculo (de centro O), es recto, e igualmente para el ángulo AED inscrito en un semicírculo (de centro O’). Por consiguiente AF y AE son dos perpendiculares a la recta CD trazadas desde A.
Puede verse inmediatamente que el trazado de la figura no es correcto: la recta CD debe pasar por B.
Notas:
[1]Zalam – quiere decir paz. Es una expresión de la que se sirven los árabes en sus saludos. Cuando un mahometano encuentra a otro lo saluda en los siguientes términos: Zalam aleikum (La paz sea contigo). Y diciendo tales palabras lleva su mano derecha al corazón. La respuesta es “Aleikum essalam” (¡Sea contigo la paz!). Cuando el saludo es dirigido a un cristiano toma, en general, otra forma: “¡Sebac el chair!” (Buen día), o bien: “¿Sabe Zalamat?” (¿Cómo está, amigo?). los cristianos son considerados infieles y no tienen derecho al Zalam (Malba Tahan).
[2] Alah o Allah – Dios. Los árabes designan al Creador por cuatrocientos noventa y nueve nombres distintos. Los musulmanes siempre que pronuncian el nombre de Dios añádenle una expresión de alto respeto y adoración. (M.T.)
[3]Khamat de Marú , ciudad situada en la base del monte Ararat, Khoy, situada en el valle del mismo nombre y bañada por las aguas que descienden de las montañas de Salmas. (Nota de Malba Tahan)
[4]Bagdalí , individuo nacido en Bagdad.
[5] Musulmán, nombre derivado de Mouslin, “aquel que se resigna a la voluntad de Dios”. Los musulmanes practican la religión de Mahoma y son actualmente unos 240 millones, aproximadamente.
[6] No pocos fueron los matemáticos que se hicieron notables por la precocidad con que revelaron sus aptitudes: Blas Pascal, a los 16 años escribió un tratado sobre las cónicas; Evaristo Galois a los 15 años comentaba obras de cálculo y análisis; José Bertrand, a los 11 años iniciaba los cursos en la Escuela Politécnica; Nicolás Enrique Abel a los 16 años descubría y demostraba teoremas de Álgebra Superior.
[7]Jamal – una de las muchas denominaciones que los árabes dan a los camellos.
[8] Este curioso resultado proviene de ser la suma
Habiendo aumentado el dividendo a 36, el sobrante resultó entonces 1/18 de 36, o sea los dos camellos referidos en el reparto hecho por el “Hombre que calculaba”.
1/2 + 1/3 + 1/9 = 17/18
menor que la unidad. De modo que el reparto de los 35 camellos entre los tres herederos no se habría hecho por completo; hubiera sobrado 1/18 de 35 camellos.Habiendo aumentado el dividendo a 36, el sobrante resultó entonces 1/18 de 36, o sea los dos camellos referidos en el reparto hecho por el “Hombre que calculaba”.
[9]Sheik – término respetuoso que se aplica, en general, a los sabios, religiosos y personas respetables por la edad o posición social.
[10]Visir – ministro –Califa- soberano musulmán. Los Califas decíanse sucesores de Mahoma.
[11]Mahoma nació en la Meca, en el año 571 y allí murió., en el año 632. Huérfano desde temprana edad fue criado primeramente por su abuelo y luego por un tío, ambos pobres; tuvo, pues, que emplearse como pastor, pasando a servir más tarde como guía para las caravanas, entrando, por fin, al servicio de una prima viuda y rica, llamada Cadidja.
[12]¡Mac Alah! (Poderoso es Dios). Exclamación usual entre los musulmanes.
[13] En la traducción, esta relación de duplicidad solo se ha conservado aproximadamente.
[14]Chamir – Jefe de caravana
[15]Dracma – moneda persa de oro
[16]Alah sea contigo - significa “Dios te proteja”
[17] Analizando este problema mediante la teoría de las interpolaciones, el resultado riguroso no es 26. en efecto, observemos que para una venta de 200 el pago era 35, es decir el 17,5 % del precio de venta; y que para una venta de 100 el pago era de 20, es decir el 20% del precio de venta.
Para cada unidad de aumento en la venta corresponde una disminución en el pago, de un [(20-17,5):100] %.
Para 40 dracmas de aumento en la venta corresponderá, pues, una disminución en el pago, de un 0.025X40=1%.
El pago que corresponde a 140 es, pues, el 20-1=19% del precio de venta, o sea, 140 x 19:100=26,6, y no 26 como indicó nuestro protagonista.
Para cada unidad de aumento en la venta corresponde una disminución en el pago, de un [(20-17,5):100] %.
Para 40 dracmas de aumento en la venta corresponderá, pues, una disminución en el pago, de un 0.025X40=1%.
El pago que corresponde a 140 es, pues, el 20-1=19% del precio de venta, o sea, 140 x 19:100=26,6, y no 26 como indicó nuestro protagonista.
[18]Almenara – torre que tienen las mezquitas. Desde las almenaras, o “minaretes”, el muecín llama a los fieles a la oración.
[19] Las oraciones obligatorias para los musulmanes en el día, son cinco. La primera al amanecer; la segunda al medio día; la tercera a las 16 horas, más o menos; la cuarta a la puesta del Sol y la última por la noche. Cada oración debe ser precedida por abluciones.
[20] Son tres letras notables y de uso corriente en el alfabeto árabe. La última no puede ser pronunciada correctamente por los latinos; es una especie de “A” sorda y gutural que sólo los orientales reproducen con perfección.
[21] Si los camellos fuesen, por ejemplo, 10, el total de patas y orejas (6 para cada uno) sería de 60. Es por ello que el número de camellos se pueden obtener dividiendo por 6 el de patas y orejas.
[22] Número primo es aquel que sólo es divisible por sí mismo y por la unidad. El número 256 es igual al producto
2 x 2 x 2 x 2 x 2 x 2 x 2 x 2, esto es, igual a 2 elevado a la octava potencia, 28.
2 x 2 x 2 x 2 x 2 x 2 x 2 x 2, esto es, igual a 2 elevado a la octava potencia, 28.
[23]Mirza – Vocablo persa que quiere decir, literalmente, “nacido de visir” o sea “noble hidalgo”. Beremís, por ser de origen persa, daba al visir el honroso título de mirza.
[24]Suque – Lugar o calle en la que se encuentran las tiendas y casas de los mercaderes.
[25]Cafetán – Túnica galoneada. Entre los persas era un ropaje o túnica que usaban habitualmente.
[26]Dijins – Genios bienhechores, en cuya existencia creían los árabes. Actualmente esa creencia sólo existe en las clases incultas. Existían también los refrites que eran genios malignos.
[27] Uassalam – Fórmula usual de despedida (M.T.)
[28] Palabras atribuidas a Platón.
[29] El camello presenta una rareza. Es el único mamífero, que tiene los glóbulos de la sangre de forma elíptica. Los naturalistas señalan esa forma como característica de las aves y los reptiles.
[30] Esa curva es la parábola.
[31] Sunita – Individuo de una de las sectas musulmanas. Adepto a la doctrina de “Sunnat” es, en general, contrario a cualquier manifestación de arte (M. T.)
[32] Frase de Platón.
[33] La segunda solución es la siguiente: 1.er socio: 3 vasos llenos, 1 vaso medio lleno y 3 vasos vacíos; al 2.o socio: 3 vasos llenos, 1 vaso medio lleno y 3 vasos vacíos; y al 3. er socio: 1 vaso lleno, 5 medio llenos y 1 vaso vacío.
[34] Filósofo, matemático y médico. Al-Hossein es más conocido por Avicena. Nació en Chiraz, en Persia, en el año 980 y fue muerto a traición, por los alrededores de Hamadam (1057). Al-Hossein era llamado por los árabes El príncipe de los médicos. Una de sus obras de medicina fue adoptada por la Escuela de Montpellier, en tiempos de Luis XIV. Al-Hossein fue el primero en proponer la prueba del 9 como verificación para las operaciones elementales.
[35] Especie de acacia.
[36] El Corán prescribe cruel pena: la amputación de la mano derecha del ladrón (M. T.)
[37]Telassim – Talismán.
[38]Ulema – hombre dotado de gran cultura. Sabio.
[39]Harem – parte de la casa en que viven encerradas las mujeres.
[40]Mactub (estaba escrito). Participio pasivo del verbo catab (escribir). Expresión que traduce bien el fatalismo musulmán.
[41] “Idomeg” – planta de hojas largas y lisas.
[42] La expresión “el-hadj”, cuando precede a un nombre, indica, que la persona ya fue en peregrinación a la Meca. (M.T.)
[43]Sufi – secta musulmana de Persia.
[44] Referíase, con escarnio, a la posada donde vivía Beremís.
[45] Los números perfectos pares están dados por la siguiente expresión: 2m-1 x (2m - 1), en la que el factor (2 m - 1) debe ser un número primo. Así por ejemplo los seis primeros números perfectos que se obtienen con la fórmula, resultan de hacer m = 2, 3, 5, 7, 13, 17, y son, respectivamente, los siguientes:
6, 28, 496, 8.128, 33.550.336, 8.589.869.056
Ya hubo un matemático que se tomó el trabajo de calcular el número perfecto que resulta haciendo m = 6, obteniendo:2 658 455 991 569 831 744 654 692 615 953 842 176
[46] Las palabras citadas, bajo forma de verso, son de la primera epístola de San Pablo a los Corintios. (M. T.)
[47]Nazareno – Denominación que los árabes daban a los cristianos. (M. T.)
[48]Antar o Antara – poeta árabe anterior al Islamismo. Se hizo famoso por haber sido presentado como símbolo de coraje, audacia y caballerosidad en la célebre epopeya árabe “Romance de Antar”. Antar el poeta y su apasionada Abla, son los héroes legendarios de Arabia.
[49]Quíder o Quidr, genio dotado de gran sabiduría que, según la creencia de los árabes, vivía en la tierra para enseñar y orientar a los profetas (M. T.)
[50]Astrail – Angel de la muerte.
[51] Cabe recordar aquí la frase de Napoleón: “El progreso de un pueblo depende exclusivamente del desenvolvimiento de la cultura matemática”
[52] Esa curva hoy es perfectamente conocida; se llama catenaria.
[53] La traducción sería “Puerta en arcada”. Es extraño que M. T. no quisiese dar a esa curva el nombre por el cual era conocida por los árabes del tiempo de Beremís.
[54] En lenguaje vulgar con la palabra círculo se designa la curva, es decir, la circunferencia.
[55]Alevequil – Intendente.
[56] ¡Preparaos para la oración!
[57]Almenara – Ver nota del capítulo V.
[58] ¡Dios os guíe, señor!
[59] “Besar la tierra entre las manos” es una expresión simbólica.
[60]Sejid es un título de honor que es concedido a los príncipes descendientes de Mahoma. Aquellos que se dicen descendientes del fundador del Islamismo se juzgan con derecho al título de “ cherif” o “sejid”. El cherif, cuando ejerce cargo de gran prestigio, recibe el título de emir. Cherif es, en general, cualquier persona de origen noble. (M. T.)
[61]Djalcianas – esclavas de origen español (M. T.)
[62]Adjamis – significa “”joven de otras tierras. (M. T.)
[63]Iclimia – nombre atribuido a la hija más vieja de Eva. Iclimia, según la tradición árabe, es más joven que Caín. (M. T.)
[64]Tabessan – pequeña (M. T.)
[65] Título dado exclusivamente a los descendientes de Mahoma. (M. T.)
[66]Rabindranath Tagore (1861 - 1941), el gran poeta, pensador y educador indio, nacido en Calcuta. Fue educado en la secta Brama – Samay, fundada por su padre, gran reformador religioso, que trató de unificar los principios de los Vedas con el sentimiento cristiano. El Premio Nobel, que obtuvo en 1913, mereció para él la atención universal. Tagore fue el poeta que más haya hecho conocer la sensibilidad del oriente contemporáneo a las mentalidades occidentales.
Su aspecto venerable y sus viajes contribuyeron a difundir su obra, respetada en todo el mundo. Era un extraordinario sentidor de la paz y de la naturaleza, conceptos en los que basó las directivas de su célebre escuela de Bolpur. Su principal obra es Gitanjali (La Ofrenda Lírica). Otras producciones: El Jardinero,Pájaros Perdidos, La Cosecha,El Asceta Sanyasi, Salón Oscuro,Ciclo de la Primavera, Chitra,La Hermana Mayor y otros cuentos.La Escuela del Papagayo, Nacionalismo, Gora, A Cuatro Voces, La Religión Del Hombre, etc., etc.
Su aspecto venerable y sus viajes contribuyeron a difundir su obra, respetada en todo el mundo. Era un extraordinario sentidor de la paz y de la naturaleza, conceptos en los que basó las directivas de su célebre escuela de Bolpur. Su principal obra es Gitanjali (La Ofrenda Lírica). Otras producciones: El Jardinero,Pájaros Perdidos, La Cosecha,El Asceta Sanyasi, Salón Oscuro,Ciclo de la Primavera, Chitra,La Hermana Mayor y otros cuentos.La Escuela del Papagayo, Nacionalismo, Gora, A Cuatro Voces, La Religión Del Hombre, etc., etc.
[67]Mhazma – Especie de pollera que llevan las bailarinas.
[68]Haquim – Médico a quien el rey confía la asistencia de sus esposas (M. T.)
[69] Ya Condorcet observaba: “El marino, a quien la exacta determinación de la longitud preserva del naufragio, debe la vida a una teoría concebida hace veinte siglos por hombres de genio, que sólo tenían en vista especulaciones geométricas”.
[70]Al – Carismi –geómetra árabe.
[71] Véanse los cuadrados mágicos que citamos en el apéndice de este libro, entre las “Curiosidades Matemáticas”
[72] Militares – una de las cuatro castas en que se divide el pueblo hindú (M. T.)
[73]Radj – Jefe militar.
[74]Vedas – El más antiguo monumento de la literatura sánscrita que comprende los cuatro libros sagrados del bracmanismo, cuyos nombres, por orden de antigüedad, son: Rig Veda; Sama Veda; Yogur Veda, y Atarva Veda.
[75] Esclavo.
[76] Diosa.
[77] Segundo miembro de la trinidad brahmánica.
[78] Nombre del inventor del juego de ajedrez. Significa “natural de Lahur.”
[79] Los elefantes más tarde fueron sustituidos por las torres.
[80] Los visires son las piezas llamadas alfiles.
[81] Individuo de una de las castas de Choromandel. Corresponde, en la escala social, a la casta de los polcas.
[82] Ese número contiene 20 guarismos y es el siguiente: 18.446.744.073.709.551.615. se obtiene restando 1 a la potencia 64ª de 2, o sea: (264 – 1).
[83]Ceira o cer – Unidad de capacidad y de peso, usada en la India. El valor de la ceira varía de una localidad a otra.
[84] Cadis – Jueces. Denominación dada, en general, a los magistrados.
[85] El lector encontrará, en este singular romance, varias referencias a los meses que constituían el año musulmán. Conviene observar que no existe correspondencia entre el año musulmán y el gregoriano, pues los árabes adoptaron el año lunar, que es 11 días más corto que el año solar. Conviene notar, pues, que el siglo musulmán equivale, en realidad, a 97 años. Los doce meses árabes son: Muharrem, Safar, Bavi - elaval, Rabietsani, Ajumada elula, Ajumada Etsania, Radjab, cha – band, Ramadan, Chaval, Dzoul – cad y Dzoul – hidjdj.
[86] El ratl vale una centésima parte de 15 Kg. El abás es una unidad de peso empleada en la evaluación de perlas. El cate es una pesa usada en la China y equivale á 625 gramos.
[87] Jefe de los narradores de cuentos (Ver: De Amicis)
[88]Imman – Hombre religioso encargado de leer el Corán en la mezquita.
[89]Masudí – Cuentista árabe notable: amigo y compañero de Mahoma. Escribió: “Moroudj edls - Dhanab”, obra de larga repercusión traducida al francés como “Praderas de oro”. Murió en el año 951.
[90]Sob - parte de la mañana.
[91] Pitagóricos – geómetras griegos, discípulos de Pitágoras
[92] la expresión de Suba-Sultra es:
que da el valor 1,414215.
que da el valor 1,414215.
[93]Senos – números empleados en Matemática y que aparecen en Trigonometría; el seno de un ángulo agudo de un triángulo rectángulo es igual a la razón entre las medidas del cateto opuesto a dicho ángulo y la hipotenusa.
[94] El volumen de la pirámide es un tercio de la base por la altura.
[95] Por la regla de Aria-Bata, el valor p de los hindúes se expresaba con la fracción 62.832 / 20.000 que corresponde al número 3,1416.
[96] Era de los mahometanos, que se cuenta desde la puesta del Sol del jueves 15 de julio de 662, día de la huida de Mahoma de la Meca a Medina, y que se compone de años lunares de 354 días, intercalando once de 355 en cada período de treinta.
[97] La división por cero no tiene sentido.
[98] El número es 28.
[99] Nombre antiguo de Ceilán.
[100]Catil , moneda; unidad de peso.
[101] Recaudador
[102] En el enunciado de Báskara, el número 79 resuelve el problema, pero no para el caso referido, que “el número de monedas fuese más de 200 y menos de 300”.
[103] Importante centro de comercio de perlas.
[104] Hamilton.
[105] Kant.
[106] Definiciones dadas por matemáticos famosos: 1. Baltzer; 2. Kambly; 3. Schuler; 4. Brenner; 5. Boutroux; 6. Sodré da Gama.
[107] Existen, en Matemática, varios conceptos que no tienen definición. Magnitud, espacio, recta, superficie, etc.
[108] En francés (quatre vingh).
[109] Divisores de 12: 12, 6, 4, 6, 2 y 1. Divisores de 10: 15, 5, 2 y 1.
[110]Guijarro , en latín, es cálculi.
[111] La palabra cero, viene del árabe sifr, vacío, que es la traducción del sánscrito sunia. El vocablo sifr se tradujo por cifra. La forma cero se originó en dos vocablos zefu y zéfiro, siendo esta última encontrada en una obra de Leonardo Pizano, geómetra notable que vivió en el siglo XII.
[112] Esos versos son de Tagore.
[113] La mayor notabilidad de la antigua ciencia musulmana. En sus libros estudiaron medicina muchas generaciones.
[114] Los matemáticos árabes no disponían de nombres para designar los términos de las fracciones (M. T.)
[115] Mme. Staël; Pitágoras; Corneille.
[116] Ese resto de vida será x – 8 (de la vida descontamos los 8 años ya transcurridos).
[117] ¿Para dónde? (¿Para dónde me van a llevar?)
[118] Leyenda árabe.
[119] Para resolver algebraicamente el problema llamamos x al número de perlas a repartir, e igualando la expresión del número de perlas que le toca a la primera hija con la de la segunda, obtenemos la ecuación
que resuelta nos da, x 36 perlas. El número de hijas es:
que resuelta nos da, x 36 perlas. El número de hijas es:
[120] Mujeres muy viejas que frecuentan los harenes y llevan informaciones a los pretendientes sobre los atributos y dotes de las jóvenes casaderas.
[121] Dividamos un segmento de 80 cm (por ejemplo) en dos partes midiendo, respectivamente, 49,4 cm y 30,6 cm Tenemos, entonces: 80 : 49,4 = 49,4 : 30,6
De ahí la proporción:
Segmento total : Parte mayor = Parte mayor : Parte menor
Esta notable división se llama división áurea o división en media y extrema razón.
De ahí la proporción:
Segmento total : Parte mayor = Parte mayor : Parte menor
Esta notable división se llama división áurea o división en media y extrema razón.
[122] El valor de la relación 809/500 es un número decimal 1,1618. Beremís halló para la joven Zaira el número 1,616 que difiere en dos milésimos del resultado más aproximado antes indicado.
[123] El profesor norteamericano George Birkhoff, en recientes conferencias dadas en capitales sudamericanas (1942), indicó la “posibilidad de una medida estética”, ya sea en las Bellas Artes, en la Música, etc., y dio, para la medida de la belleza, la fórmula siguiente:
Bello = Orden / Complejidad
[124] En el lenguaje algebraico, representando con x la edad de Diofanto, se tiene la ecuación:
x/6 + x/12 + 5 + x/2 + 4 = x, de donde x = 84 años.
[125] 17, 18 y 26, sin ser cubos perfectos, presentan propiedades idénticas en relación a los guarismos de sus cubos.
[126] Mes de cuaresma musulmán.
[127] ¡Dios es grande!
[128]Fatihat – Primer capítulo del Corán, contiene 7 versículos. El vocablo fatihat significa: “aquel que abre” (M. T.)
[129] Jesús Cristo.
[130] Nació en el año 275 antes de Cristo. Fue el fundador de la Geodesia.
[131]Suhhel , nombre que los árabes dan a la estrella Sirius. La estrella Polar es denominada Dsjudde. La Vía Láctea, para los musulmanes, es Nahr e-Mudsjerra. (M. T.)
[132] Nació en 1200 y murió, a consecuencia de la caída de un camello, en 1280. Escribió “Tratado de los instrumentos astronómicos”.
[133] El producto 55 X 55 es igual a 3025.
[134]Edduhhr – medio día. Los árabes dividen los días en 24 horas, que cuentan a partir del momento en que se pone el sol. Así, para los árabes, la noche del 13 es aquella que transcurre entre los días 12 y 13. La hora en que el sol se pone se llama “mogreb”; dos horas más tarde “elascha”; la segunda hora después de “mogreb” es llamada “elmarfa”. La media noche es, para los musulmanes, “nusfel-leil”. La aurora “elfedsjer”. La hora del almuerzo (9 de la mañana) es llamada “el-ghudda”; al medio día “eddhuhhr”; tres horas más tarde, “ el-arr”. (M. T.)
[135] Cristianos.
[136] El diluvio duró 40 días y 40 noches; 40 años emplearon los judíos para alcanzar la Tierra de Promisión; 40 días estuvo Jesús en el desierto.
[137] El más admirado de los poemas árabes antiguos. Fue escrito por el célebre poeta Mouaid Eddine Elhoussein ben Alí ben Mohamed ben Abdessamad Elosfihai Etourrai. (M. T.)
[138] Vivió en el año 420 A.C.
[139] Parte de la Mecánica que estudia el movimiento de los cuerpos en sus relaciones con el espacio y el tiempo, prescindiendo de la idea de fuerza.
[140] La solución geométrica de un problema con el uso exclusivo de la regla y el compás, es llamada solución “euclidiana”. Un problema es denominado “euclidiano” cuando solamente se puede resolver con la regla y el compás.
[141] El número que expresa la relación entre la circunferencia y el diámetro es designado en Matemática con la letra π.
[142] La conquista de Bagdad por las hordas salvajes de Hulagú es descrita por varios historiadores. La ciudad fue bárbaramente saqueada por los invasores. Todo fue arrasado y destruido; el fuego consumió los grandes palacios y las más ricas mezquitas. La sangre de los muertos inundaba las calles y las plazas. Los mongoles arrojaron al Tigres todos los libros de las grandes bibliotecas y los preciosos manuscritos, mezclados con el barro, formaron un puente sobre el que los conquistadores pasaban a caballo.
Mg. Edgar Zavaleta Portillo
Sub Dirección de Administración.
